
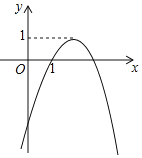
【题目】如图,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,①abc<0,②2a+b>0,③a-b+c<0,④b2>4ac,⑤关于x的方程ax2+bx+c-2=0没有实数根.则下列结论正确的有______.(填序号)
【答案】②③④⑤
【解析】
由抛物线开口方向得到a<0,由抛物线的对称轴方程得到b=-2a>0,由抛物线与y轴的交点位置得到c<0,则可对①进行判断;利用抛物线的对称轴方程可对②进行判断;根据函数的图象可对③进行判断;根据判别式的意义可对④进行判断;利用二次函数的最大值为1可对⑤进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-![]() >1,
>1,
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①错误;
∵抛物线的对称轴为直线x=-![]() >1,a<0,
>1,a<0,
∴-b<2a,
∴2a+b>0,所以②正确;
由图象可知:当x=-1时,y<0,
∴a-b+c<0,所以③正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,所以④正确;
∵函数的最大值为1,
∴y=ax2+bx+c(a≠0)的图象与直线y=2没有交点,
∴方程ax2+bx+c-2=0没有实数根,所以⑤正确.
故答案为:②③④⑤.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+8分别交x轴,y轴于点A,B,直线y![]() x+3交y轴于点C,两直线相交于点D.
x+3交y轴于点C,两直线相交于点D.

(1)求点D的坐标;
(2)如图2,过点A作AE∥y轴交直线y![]() x+3于点E,连接AC,BE.求证:四边形ACBE是菱形;
x+3于点E,连接AC,BE.求证:四边形ACBE是菱形;
(3)如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG,FG,当CG=FG,且∠CGF=∠ABC时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知![]() 年投资
年投资![]() 万元,预计
万元,预计![]() 年投资
年投资![]() 万元.若这两年内平均每年投资增长的百分率相同.
万元.若这两年内平均每年投资增长的百分率相同.
![]() 求平均每年投资增长的百分率;
求平均每年投资增长的百分率;
![]() 按此增长率,计算
按此增长率,计算![]() 年投资额能否达到
年投资额能否达到![]() 万?
万?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时开始攀登一座900 m高的山,第一组的攀登速度是第二组的1.2倍,他们比第二组早30 min到达顶峰.
(1)求这两个小组的攀登速度各是多少?
(2)如果山高为a m,第一组的攀登速度是第二组的b倍,并比第二组早t min到达顶峰,则两个小组的攀登速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
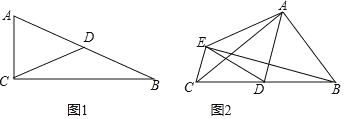
灵活应用:如图2,△ABC中,∠BAC=90°,AB=3, AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE, CE.
(1)求AD的长;
(2)判断△BCE的形状;
(3)求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
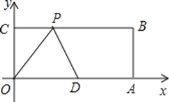
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 、
、![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上运动,当
边上运动,当![]() 是以腰长为5的等腰三角形时,点
是以腰长为5的等腰三角形时,点![]() 的坐标为________________.
的坐标为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
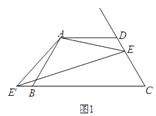
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
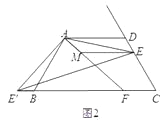
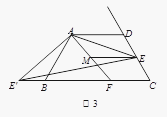
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com