Question

如图所示，已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一条直线，且B，C在AE的异侧，BD⊥AE于D，CE⊥AE于E．

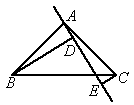
(1)求证BD=DE＋CE；

(2)若直线AE绕A点旋转到如图所示的位置时(BD＜CE)，其余条件不变，则BD与DE，CE的关系如何？直接写出结果；

(3)若直线AE绕A点旋转到如图所示的位置时(BD＞CE)，其余条件不变，则BD与DE，CE的关系怎样？直接写出结果．

Answer 1

答案：略
解析：

证明：(1)∵∠BAC=90°，BD⊥AE， ∴∠BAE＋∠EAC=90°，∠ABD＋∠BAE=90°， ∴∠ABD=∠EAC， 又AB=AC，∠BDA=∠AEC=90°， ∴△ABD≌△CAE， ∴BD=AE，AD=CE， 又∵AE=AD＋DE， ∴BD=AE=DE＋CE． 解：(2)BD=DE－CE． (3)BD=DE－CE．

提示：

(1)由已知出发容易得到：BD=AE，再分析观察AE=AD＋DE，又易证AD=EC． (2)猜想规律，再运用几何知识证明．