
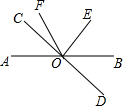
 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.  一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
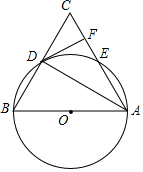 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(x-1)=1-2(2+3x) | B. | 3(x-1)=1+2(2x+3) | C. | 3(x-1)=6-2(2x+3) | D. | 3(x-1)=6+2(2x+3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
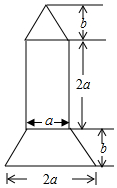 2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,.
2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
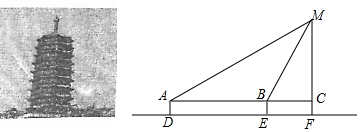
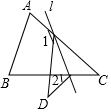 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )| A. | 140° | B. | 90° | C. | 80° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com