
【题目】如图,△ABC中,AB=AC, ∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,
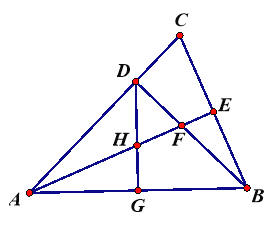
(1)求∠ACB的度数;
(2)HE=![]() AF
AF
【答案】
【解析】
试题分析:(1)利用等边对等角可证:∠ACB=∠ABC,根据三角形内角和定理可以求出∠ACB的度数;
(2)连接HB,根据垂直平分线的性质可证AE⊥BC,BE=CE,再根据ASA可证:Rt△BDC≌Rt△ADF,根据全等三角形的性质可证:BC=AF,从而可以求出HE=BE=![]() BC,因为AF=BC,所以可证结论成立.
BC,因为AF=BC,所以可证结论成立.
试题解析:(1)∵AB=AC,
∴∠ACB=∠ABC,
∵∠BAC=45°,
∴∠ACB=∠ABC=![]() (180°-∠BAC)=
(180°-∠BAC)=![]() (180°-45°)=67.5°;
(180°-45°)=67.5°;
(2)连结HB,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,BE=CE,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CAE=∠CBD,
∵BD⊥AC,D为垂足,
∴∠DAB+∠DBA=90°,
∵∠DAB=45°,
∴∠DBA=45°,
∴∠DBA=∠DAB ,
∴DA=DB,
在Rt△BDC和Rt△ADF中,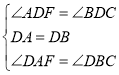
∴Rt△BDC≌Rt△ADF (ASA),
∴BC=AF,
∵DA=DB,点G为AB的中点,
∴DG垂直平分AB,
∵点H在DG上,
∴HA=HB,
∴∠HAB=∠HBA=![]() ∠BAC=22.5°,
∠BAC=22.5°,
∴∠BHE=∠HAB +∠HBA =45°,
∴∠HBE=∠ABC-∠ABH=67.5°-22.5°=45°,
∴∠BHE=∠HBE,
∴HE=BE=![]() BC,
BC,
∵AF=BC,
∴HE=![]() AF.
AF.



科目:初中数学 来源: 题型:
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.

(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
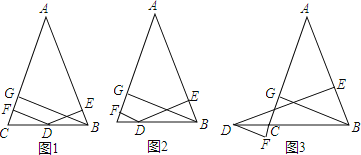
(1)、如图1,若D是BC边上的中点,∠A=45°,DF=3,求AC的长;
(2)、如图2,D是线段BC上的任意一点,求证:BG=DE+DF;
(3)、在图3,D是线段BC延长线上的点,猜想DE、DF与BG的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
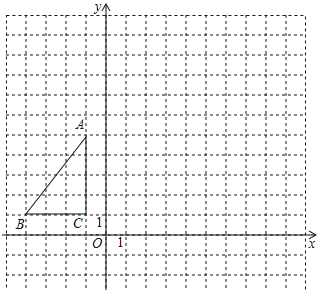
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com