
分析 首先化简($\frac{1}{x}$-$\frac{2}{x-1}$)÷$\frac{{x}^{2}+x}{1-2x+{x}^{2}}$,然后根据x的值从不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1>0}\\{2(x-1)≤x}\end{array}\right.$的整数解中选取,求出x的值是多少,再把求出的x的值代入化简后的算式,求出算式的值是多少即可.
解答 解:($\frac{1}{x}$-$\frac{2}{x-1}$)÷$\frac{{x}^{2}+x}{1-2x+{x}^{2}}$
=$\frac{-(x+1)}{x(x-1)}$÷$\frac{{x}^{2}+x}{1-2x+{x}^{2}}$
=$\frac{1-x}{{x}^{2}}$
解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1>0}\\{2(x-1)≤x}\end{array}\right.$,
可得:-2<x≤2,
∴x=-1,0,1,2,
∵x=-1,0,1时,分式无意义,
∴x=2,
∴原式=$\frac{1-2}{{2}^{2}}$=-$\frac{1}{4}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
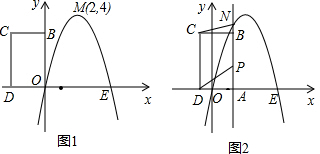
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
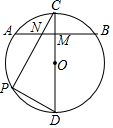 如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )
如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )| A. | (2017,0) | B. | (2017,$\sqrt{3}$) | C. | (2017,-$\sqrt{3}$) | D. | (2016,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
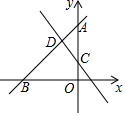 如图,直线y=kx+4(k≠0)与x轴,y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积$\frac{3}{2}$.
如图,直线y=kx+4(k≠0)与x轴,y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
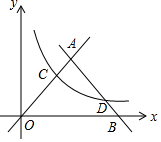 在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.
在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
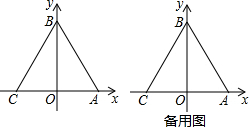
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 矩形的对角线互相垂直 | |
| C. | 四边相等的四边形是菱形 | |
| D. | 一组对边平行的四边形是平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com