练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

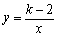    下列命题中 ①对角线相等且互相垂直的四边形是菱形；②若，那么sinɑ＞cosɑ③一正多边形的一个外角是45°，则此图形是正八边形；④若式子有意义，则x＞1；⑤在反比例函数中，若x＞0 时，y随x的增大而增大，则k的取值范围是k＞2；其中假命题有（  ）

    A．1个         B．2个           C．3个         D．4个


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


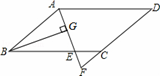
    如图，在?ABCD中，AB=6cm，AD=9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4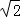cm，则EF+CF的长为　 　；



    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一个圆锥的主视图是腰长为5，底边长为6的等腰三角形，则该圆锥的侧面积是（　　）

    　

    A．

    15π

    B．

    20π

    C．

    24π

    D．

    30π

    查看答案和解析>>

    科目：初中数学 来源： 题型：


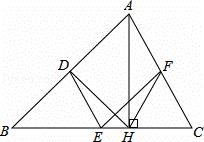
    如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．

    （1）求证：四边形ADEF是平行四边形；

    （2）求证：∠DHF=∠DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（       ）

     A．AB∥DC，AD∥BC  B．AD∥BC ∠ABC=∠ADC

     C．AO=CO，BO=DO  D．AB∥DC，AD=BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知ab=-8，若﹣2≤b，则a的取值范围是              

    查看答案和解析>>

    科目：初中数学 来源： 题型：


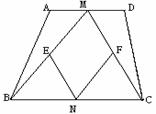
    如图，在等腰梯形ABCD中，M、N分别为AD、BC的中点，E、F分别为BM、CM的中点。          

    （1）求证：△ABM≌△CDM；

    （2）判断并证明四边形MENF是何种特殊的四边形；

    ‚当等腰梯形ABCD的高h与底边BC满足怎样的数量关系时，四边形MENF是正方形？（直接写出结论，不需要证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


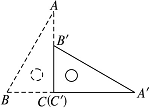
    如图，直角三角板ABC的斜边AB＝12 cm，∠A＝30°，将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使点B′落在原三角板ABC的斜边AB上，则三角板A′B′C′平移的距离为           

    查看答案和解析>>

    科目：初中数学 来源： 题型：


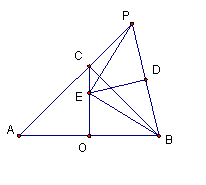
     如图，AB为等腰直角⊿ABC的斜边（AB为定长线段），O为AB的中点，P为AC延长线上的一个动点，线段PB的垂直平分线交线段OC于点E，D为垂足，当P点运动时，给出下列四个结论，其中正确的个数是(     )

    ①E为⊿ABP的外心；　 　②∠PEB=90°；

    ③PC·BE = OE·PB；    ④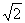CE + PC=．

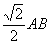    A．1个      B．2个       C．3个       D．4个

    查看答案和解析>>

    同步练习册答案