
����Ŀ����֪�����κ���y=x2+2mx+2n����x����A,B����(A��B�����)
��1����m=3ʱ��n=4ʱ�� ����A��B�������ꣻ�ڽ�����������ƽ��k����λ��x����M��N��M��N����ࣩ����B��M���ȷ�AN��ֱ��д��k��ֵ��
��2����m=1ʱ�����߶�AB������ֻ��5����ĺ�����Ϊ��������n��ȡֵ��Χ��
��3����A(x1,0)��B(x2,0)����m��n��������ʱ��x1��x2�ܷ��������������ܣ��������֤�������ܣ���˵������.
���𰸡�(1)�� (-4,0)��(-2,0)���� 1 �� (2)-4��n��![]() ��(3)������
��(3)������
��������
(1)�ٵ�m=3ʱ��n=4ʱ�����κ�������ʽΪy=x2+6x+8����y=0���ⷽ�̼��ɽ�����⣮
�ڸ������������M�����꼴�ɽ�����⣮
(2)�������֪��x=1ʱ��y��0��x=2ʱ��y��0���г�����ʽ���ɽ�����⣮
(3)��m��n��������ʱ��x1��x2�����������������÷�֤��֤�����ɣ�
�⣺��1����m��3ʱ��n��4ʱ�����κ�������ʽΪy��x2+6x+8��
����y��0�õ�x2+6x+8��0�����x����2��4����A����4��0����B����2��0����
�ʴ�Ϊ��A(-4,0),B(-2,0).
�ڡ�����������ƽ��k����λ��x����M��N��M��N����ࣩ��
B��M���ȷ�AN��AB��2��
��AM��BM��1��
��M����3��0������k��1��
�ʴ�Ϊ��k=1.
��2����m��1ʱ�������ߵĶԳ���x����1��
���߶�AB������ֻ��5����ĺ�����Ϊ��������Щ����Ϊ��3����2����1��0��1��
��x��1ʱ��y��0��x��2ʱ��y��0��
��![]() ����ã�-4��n��
����ã�-4��n��![]() ��
��
�ʴ�Ϊ��-4��n��![]() ��
��
��3����m��n��������ʱ��x1��x2����������������
���ɣ�����m��n��������ʱ��x1��x2����������
��x1x2��2n��
��x1��x2�п϶�һ����������һ����ż����
��x1+x2һ����������������x1+x2=-2m��ż���������ì�ܣ�
����費������
�൱m��n��������ʱ��x1��x2����������������
�ʴ�Ϊ����m��n��������ʱ��x1��x2����������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������лֱ��A��B����ͬʱ����ʻ�����׳�����B�ǣ��ҳ�����A�ǣ�����ī���ڸǣ�ͼ���ṩ����������B�ǵ�·��S����ǧ�ף���S����ǧ�ף�����ʻʱ��t��ʱ���ĺ���ͼ���һ���֣�

��1���ֱ����S����S����t�ĺ�����ϵʽ������д��t��ȡֵ��Χ����
��2����A��B����֮��ľ��룬��tΪ��ֵʱ����������
��3�����������300ǧ��ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��Թ̶�����һ���Թ���һ����Ʒ��3�·ݰ�һ���ۼ����ۣ����۶�Ϊ2400Ԫ��Ϊ�������������ٿ�棬4�·���3�·��ۼۻ����ϴ�9�����ۣ��������������30�������۶�����840Ԫ��
��1������̵�3�·�������Ʒ���ۼ��Ƕ���Ԫ��
��2��������̵�3�·�����������Ʒ������Ϊ900Ԫ����ô���̵�4�·�����������Ʒ�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020�������п��������˿������뿼����������¼���Ҫ���߲���Ϊ�˽�ѧ��������뿼��������¼��������������һ��ѧУij�����翼�����뿼����ۼ�����![]() ���ˣ���ʱ��
���ˣ���ʱ��![]() �����ӣ��ı仯������������±���������9-15��ʾ
�����ӣ��ı仯������������±���������9-15��ʾ![]() ��
��
ʱ�� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
���� | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
��1��������15�����ڿ������뿼����ۼ�������ʱ��ı仯���ɣ����ó�����ѧ����֪ʶ���![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���������һ������Ϳ�ʼ�������£����¼�����2����ÿ������ÿ���Ӽ��20�ˣ������ŶӲ������£����Ŷ��������ʱ�ж����ˣ�ȫ��������������¼����Ҫ����ʱ�䣿
��3���ڣ�2���������£����Ҫ��12��������ȫ������������¼�⣬��һ��ʼ��Ӧ���������Ӽ������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
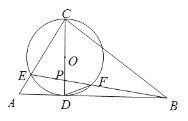
����Ŀ����ͼ����ABC�У���ACB��90����DΪAB�ϵ�һ�㣬��CDΪֱ���ġ�O��AC��E������BE��CD��P������O��F������DF����ABC����EFD��
(1)��֤��AB���O���У�
(2)��AD��4��BD��6�����O�İ뾶�� ��
(3)��PC��2PF��BF��a����CP(��a�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�ABΪֱ������CΪԲ��һ�㣬�ӳ�AB����D��ʹCD=CA����![]() ��
��

��1����֤��![]() �ǡ�O�����ߣ�
�ǡ�O�����ߣ�
��2���ֱ��A��B������ֱ��CD�Ĵ��ߣ�����ֱ�ΪE��F���㣬��C����AB�Ĵ��ߣ�����Ϊ��G����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
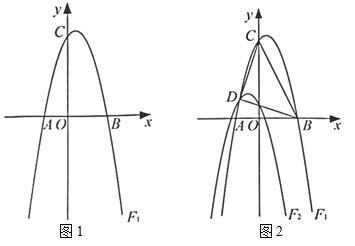
����Ŀ����ͼ1��ʾ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() �͵�
�͵�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1����������![]() �ı���ʽ��
�ı���ʽ��
��2����ͼ2����������![]() ������ƽ��1����λ��������ƽ��3����λ���õ�������
������ƽ��1����λ��������ƽ��3����λ���õ�������![]() ����������
����������![]() ��������
��������![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��
�����![]() �����ꣻ
�����ꣻ
���ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3���ڣ�2���������£�������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊ����ֱ�������Σ������ڣ������
Ϊ����ֱ�������Σ������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
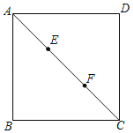
����Ŀ����ͼ����������ABCD�У���E��F���Խ���AC���ȷ֣���AC��9����P�������εı��ϣ�������PE+PF��8�ĵ�P�ĸ����ǣ�������
A.8B.6C.4D.0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶һ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��λ��ί�Լס�����λͬѧ�IJ��ձ��ݴ�֣�����֯ȫ��50��ͬѧ�������������ͶƱ�����������µĴ�ֱ��Ͳ�����������ͳ��ͼ��
��λ��ί�Լס�����λͬѧ�IJ��ձ��ݴ�֣�����֯ȫ��50��ͬѧ�������������ͶƱ�����������µĴ�ֱ��Ͳ�����������ͳ��ͼ��
��λ��ί�Ĵ�ֱ�
A | B | C | D | E | |
�� | 89 | 91 | 93 | 94 | 86 |
�� | 88 | 87 | 90 | 98 | 92 |
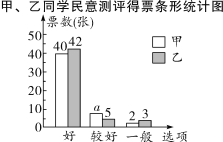
���������λ��ί�Լ�ͬѧ���ձ������������ƽ���ֺ���λ����
![]() ���֣�����λ����91��.
���֣�����λ����91��.
��1������λ��ί����ͬѧ���ձ������������ƽ���ֺ���λ����
��2��![]() ________������ȫ����ͳ��ͼ��
________������ȫ����ͳ��ͼ��
��3��Ϊ�˴Ӽס���������ֻѡ�γ�һ��ȥ�μ��������ݳ����༶�ƶ������µ�ѡ�ι���
ѡ�ι���ѡ���ۺϷ���ߵ�ͬѧ�μ��������ݳ�.���У��ۺϷ֣����շ�![]() ������
������![]() ��
��
���շ֣���λ��ί���������ȥ��һ����߷ֺ�һ����ͷ֣�����ƽ���֣������֣����á�Ʊ����2�֣����Ϻá�Ʊ����1�֣���һ�㡱Ʊ����0��
�ٵ�![]() ʱ��ͨ������˵��Ӧѡ����λͬѧȥ�μ��������ݳ���
ʱ��ͨ������˵��Ӧѡ����λͬѧȥ�μ��������ݳ���
��ͨ������˵��![]() ��ֵ�����Ƕ��٣�
��ֵ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com