
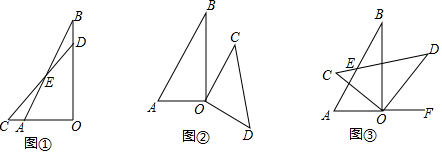
分析 (1)直接利用邻补角即可得出结论,
(2)利用平行线得出∠BOC=30°,进而得出∠AOC=120°,最后除以速度即可得出时间;
(3)先求出∠AOC=60°,进而得出∠AOD=120°,最后用四边形的内角和定理即可得出结论.
解答 解:(1)∵∠BAO=60°,
∴∠AEC=180°-∠BAO=120°;
故答案为120°;
(2)∵AB∥OC,
∴∠BOC=∠ABO=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∴120°÷20°=6秒;
即:旋转6秒时,AB∥OC;
(3)∵点F是AO延长线上,∠COD=90°,
∴∠AOC+∠DOF=90°,
∵∠DOF=2∠AOC,
∴∠AOC=30°,∠DOF=60°,
∴∠AOD=180°-∠DOF=120°,
在四边形AODE中,根据四边形的内角和得,
∠AED=360°-∠OAB-∠AOD-∠ODC=360°-60°-120°-45°=135°.
点评 此题是三角形综合题,主要考查了邻补角,平行线的性质,互余的性质,四边形的内角和定理,解(2)的关键是求出∠AOC的度数,解(3)的关键是求出∠AOD,是一道比较简单的题目.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | B. | 两直线平行,同旁内角互补 | ||
| C. | 若a2=b2,则a=b | D. | 若a2+b2>0,则a>0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-2>b-2 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | 4+3a<4+3b | D. | -2a>-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
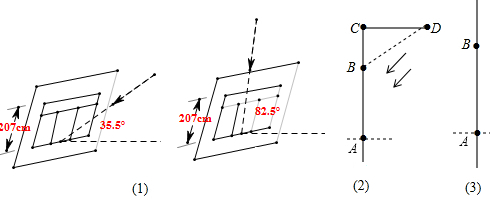
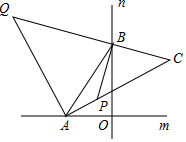 如图,直线m与直线n互相垂直,垂足为O,A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动.
如图,直线m与直线n互相垂直,垂足为O,A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
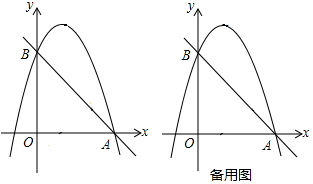
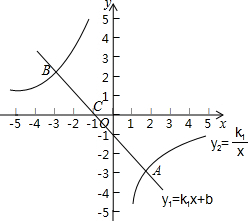 已知如图,直线y1=k1x+b与双曲线y2=$\frac{{k}_{2}}{x}$的图象相交于A(2,-3)、B(-3,m)两点.
已知如图,直线y1=k1x+b与双曲线y2=$\frac{{k}_{2}}{x}$的图象相交于A(2,-3)、B(-3,m)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com