练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
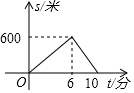
    19．小丽、小亮从学校出发到中心书城购书，小丽步行一段时间后，小亮骑自行车沿相同路线前往，两人均匀前行，他们的路程s（米）与小丽出发时间t（分）之间的函数关系如图，下列说法：①小丽的速度是100米/分；②小丽出发6分钟后小亮才出发；③学校离中心书城的路程为1000米；④小亮骑车的速度是250米/分．其中正确的是（　　）
    A．①②B．①②③C．①②④D．①③④

    分析 根据图象中的信息即可得到结论．

    解答 解：由图象知，①小丽的速度=$\frac{600}{6}$=100米/分；故①正确；
    ②小丽出发6分钟后小亮才出发；故②正确，
    ③小丽出发10分钟后与小亮相遇，所走路程为100×10=1000米，故错误；
    ④小亮骑车的速度=$\frac{1000}{10-6}$=250米/分，故正确；
    故选C．

    点评 本题考查了函数的图象，正确的识别图象是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．2016年，王先生到银行存了一笔三年期的定期存款，年利率是2.75%，若到期后取出，得到本息和 （本金+利息） 为33852元．若设王先生存入的本金为x元，则下面所列方程正确的是（　　）
    A．x+3×2.75%x=33825B．x+2.75%+=33825
    C．3×2.75%x=33825D．3（x+2.75%x）=33825

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在△ABC中，∠C为直角，∠A、∠B、∠C所对的边分别为α、b、c，且α=20，∠B=35°，解这个三角形．（精确到0.1，参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，矩形RFGD的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，且DE=2EF，△ABC中，边BC的长度为12cm，高AH为8cm，求矩形DEFG的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

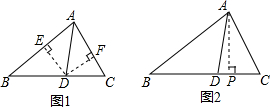    14．让我们来共同探究“三角形的角平分线”的特殊性质：
    如图，△ABC中，AD平分∠BAC，试探究S△ABD与S△ACD的比与图中线段有何关系．
    （1）下面（图1）是小明的做法，请你完成他的步骤：过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．∵AD平分∠BAC，∴DE=DF．而S△ABD=$\frac{1}{2}$AB×DE，S△ACD=$\frac{1}{2}$AC×DF．则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{（）}{（）}$；
    （2）下面（图2）是小华的做法，请你完成他的步骤：过点A作AP⊥BC，垂足为P，而S△ABD=$\frac{1}{2}$×BD×AP，S△ACD=$\frac{1}{2}$×CD×AP，则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{（）}{（）}$
    （3）结合（1）、（2）的结论，可得“三角形的角平分线”的一个新的性质：
    已知：在△ABC中，AD平分∠BAC，则线段AB、AC、BD、CD的关系为：$\frac{AB}{AC}$=$\frac{BD}{CD}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知⊙O的半径为6cm，点O到直线l的距离为5cm，则直线l与⊙O（　　）
    A．相交B．相离C．相切D．相切或相交

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如果关于x的一元二次方程ax2+bx+c=0有两个实数根，且其中一个实数根为另一个实数根的3倍，则称这样的方程为“立根方程”．
    若方程ax2+bx+c=0是立根方程，且两点P（p+p2+1，q）、Q（-p2+5+q，q）均在二次函数y=ax2+bx+c上，请求方程ax2+bx+c=0的两个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：$\frac{1}{2-a}$+$\frac{1}{2+a}$-$\frac{{a}^{2}-4a}{{a}^{2}-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．某小区9月底的房价为3.2万元/m2，同年11月底的房价为3万元/m2．设平均每月降价的百分率为 x，可列方程．（　　）
    A．3.2（1+x）2=3B．3.2（1-x）2=3C．3（1+x）2=3.2D．3（1-x）2=3.2

    查看答案和解析>>

    同步练习册答案