
����Ŀ������������5�֣���ͼ��С���ڴ�¥30��
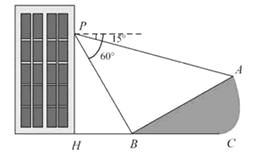
����PH��30�ף��Ĵ���P�����й۲⣬���ɽ
����A���ĸ���Ϊ15����ɽ��B���ĸ���Ϊ
60������֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��
![]() ����P��H��B��C��A��ͬһ��ƽ���ϣ���
����P��H��B��C��A��ͬһ��ƽ���ϣ���
H��B��C��ͬһ��ֱ���ϣ���PH��HC��
(1)ɽ���½ǣ�����ABC���Ķ������� �� �ȣ�
(2)��A��B�����ľ��루�����ȷ��0.1�ף��ο����ݣ�![]() ��1.732����
��1.732����
���𰸡��⣺(1)30��
(2)�����P��ˮƽ��ΪPQ����������ã�![]()
![]() 450��
450��
![]()
![]()
![]()
![]()
![]()
![]()
![]() ��A��B�����ľ���Լ34.6�ס�
��A��B�����ľ���Լ34.6�ס�
��������
���⣨1�����ݸ����Լ��¶ȵĶ��弴����⣻
��2����ֱ����PHB�У��������Ǻ����������PB�ij���Ȼ����ֱ����PBA���������Ǻ���������⣮
���������
��1����ɽ�µ��¶�i����tan��ABC��Ϊ1��![]() ��
��
��tan��ABC=![]() ��
��
���ABC=30�㣻
�ߴ�P����ɽ��B���ĸ���60�㣬
���PBH=60�㣬
���ABP=180�㩁30�㩁60��=90��
�ʴ�Ϊ��90��
��2��������ã���PBH=60�㣬
�ߡ�ABC=30�㣬
���ABP=90�㣬
���PABΪֱ�������Σ�
�֡ߡ�APB=45�㣬
��ֱ����PHB�У�PB=PH��sin��PBH=45��![]() =30
=30![]() ��m����
��m����
��ֱ����PBA�У�AB=PBtan��BPA=30![]() ��52.0��m����
��52.0��m����
��A��B�����ľ���ԼΪ52.0�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�Խ��߽���O��ֱ��m���ֱ�ֱ��AB�ڵ�E����ֱ��CD�ڵ�F����AB��4��AE��6����DF�ij���___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
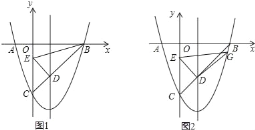
����Ŀ����ͼ����֪������y=x2��2x��3����x���ϵ�A��B���㣬��y�ύ�ڵ�C���߶�BC�������ߵĶԳ����ཻ�ڵ�D����EΪy���ϵ�һ�����㣮
��1����ֱ��BC�ĺ�������ʽ���������D�����ꣻ
��2�����E��������ΪΪm���ڵ�E���˶������У�����BDE��Ϊ�۽�������ʱ����m��ȡֵ��Χ��
��3����ͼ2������DE��������DE�Ƶ�D˳ʱ�뷽����ת90�����������߽���ΪG������EG��DG�õ�Rt��GED���ڵ�E���˶������У��Ƿ����������Rt��GED��ʹ����ֱ�DZ�֮��Ϊ2��1��������ڣ������ʱ��G�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪ���η����У���������Τ�ﶨ��������һԪ���η���![]() ���������������ʵ����
���������������ʵ����![]() ����ô
����ô![]() ��˵������������������
��˵������������������![]() �������緽��
�������緽��![]() �У�
�У�![]() �����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ
�����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ![]() ��
��![]() ����ô
����ô![]() +
+![]() =
=![]() ��
��![]()
![]() =
=![]() ,������Ķ����Ͻ�����и��⣺
,������Ķ����Ͻ�����и��⣺
��1����֪����![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() >
>![]() ,�����и�ʽ��ֵ:
,�����и�ʽ��ֵ:
��![]() ��
��![]()
��2����֪![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������
������ʵ������
���Ƿ����ʵ��![]() ��ʹ
��ʹ![]() �����������ڣ����
�����������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
����ʹ![]() ��ֵΪ������ʵ��
��ֵΪ������ʵ��![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
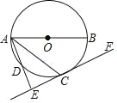
����Ŀ����ͼ��ABΪ��O��ֱ������C��D����O�ϣ��ҵ�C��![]() ���е㣬���� C��AD�Ĵ��� EF��ֱ�� AD�ڵ� E��
���е㣬���� C��AD�Ĵ��� EF��ֱ�� AD�ڵ� E��
��1����֤��EF����O�����ߣ�
��2������BC����AB=5��BC=3�����߶�AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�εIJ������̣��������ĸ����ε�ˮƽ����ı߳���Ϊa����ֱ����ı߳���b����
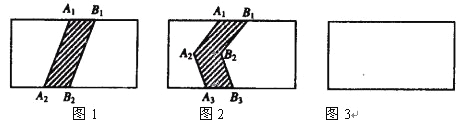
����ͼ1�У����߶�A1A2����ƽ��1����λ��B1B2���õ����ͼ��A1A2B2B1������Ӱ���֣���
����ͼ2�У�������A1A2A3����ƽ��1����λ��B1B2B3���õ����ͼ��A1A2A3B3B2B1������Ӱ���֣���
��1����ͼ3�У��������Ƶػ�һ���������۵���ߣ�ͬ������ƽ��1����λ���Ӷ��õ�һ�����ͼ�Σ�����б������Ӱ��
��2������ֱ�д����������ͼ���г�ȥ��Ӱ���ֺ�ʣ�ಿ�ֵ������
S1��__________��S2��__________��S3��__________��
��3��������̽��
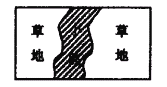
����ͼ����һ����βݵ��ϣ���һ�������İ���С·��С·�κεط���ˮƽ���ȶ���1����λ�����������հײ��ֱ�ʾ�IJݳ�������Ƕ��٣���˵����IJ�������ȷ�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֱ�Ĺ�·��������A��C��B���أ��ס�������ͬʱ�������״�A�������г�ȥB�أ�;��C����Ϣ1���ӣ�������ԭ��������B�أ�����B�غ�������ԭ·ԭ�ٷ���A�أ��Ҳ��д�B��ǰ��A�أ��ס������˾�A�ص�·��y���ף���ʱ��x���֣�֮��ĺ�����ϵ��ͼ��ʾ������ͼ�����������⣺
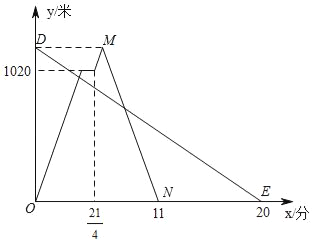
��1����д���������ٶ�Ϊ�� ����/�֣���M������Ϊ�� ����
��2�������ʱ��A�ص�·��y��ʱ��x֮��ĺ�����ϵʽ������Ҫд���Ա�����ȡֵ��Χ����
��3����ֱ��д�����˳������ڼ���A��֮ǰ�������ʱ�����˾�C�ص�·����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
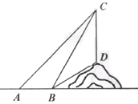
����Ŀ����ͼ��Сɽ������һ����ֱ�ڵ���ĵ��߸�![]() ��С���ӵ����ϵ�A����õ��߸˶���
��С���ӵ����ϵ�A����õ��߸˶���![]() ���������45��,�������Ե��߸���ǰ��6����B������õ��߸˶���
���������45��,�������Ե��߸���ǰ��6����B������õ��߸˶���![]() ��͵��߸˵�D������Ƿֱ���60����30��.����߸�
��͵��߸˵�D������Ƿֱ���60����30��.����߸�![]() �ĸ߶ȣ�����������ţ�
�ĸ߶ȣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼRt��ABC�У���ACB��90������B��30����AC��1����AC��ֱ��l�ϣ�����ABC�Ƶ�A˳ʱ����ת���٣��ɵõ���P1����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڣ��ɵõ���P2����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۣ��ɵõ���P3�������˹��ɼ�����ת��ֱ����P2012Ϊֹ����AP2012����_____��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com