
【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
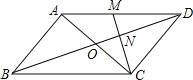
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
【答案】(1)6;(2)见解析
【解析】
试题分析:(1)根据平行四边形的性质得AD∥BC,AD=BC,OB=OD,则利用DM∥BC可判断△MND∽△CNB,所以MD:BC=DN:BN=1:2,设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,于是得到x+1=2(x﹣1),解得x=3,所以BD=2x=6;
(2)如图,在OD上截取NG=ON,延长OC到H,使HC=OC,则△HOG满足条件.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴DM∥BC,
∴△MND∽△CNB,
∴MD:BC=DN:BN,
∵M为AD中点,
∴MD:BC=1:2,
∴DN:BN=1:2,即BN=2DN,
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1),解得x=3,
∴BD=2x=6;
(2)如图,△HOG为所作.


科目:初中数学 来源: 题型:
【题目】在一个布袋中装有2个红球和2个篮球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,不放回继续再摸第二个球,求两次都摸到红球的概率;
(2)在这4个球中加入x个用一颜色的红球或篮球后,进行如下试验,搅匀后随机摸出1个球记下颜色,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到红球的概率稳定在0.80,请推算加入的是哪种颜色的球以及x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
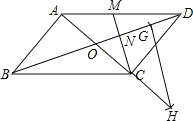
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
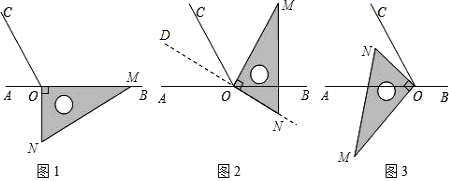
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
(1)两条直线不相交就平行
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A. 0 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
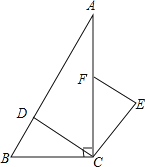
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com