
����Ŀ����һ���������������ϴ������е�A��B��C�����е�A����B�ľ���Ϊ2����C����B�ľ���Ϊ8����ͼ��ʾ�����A��B��C����Ӧ�����ĺ���m��
��1������BΪԭ�㣬���C����Ӧ�������� ��������CΪԭ�㣬��m��ֵ���� ����
��2����ԭ��O��ͼ�������ϣ��ҵ�C��ԭ��O�ľ���Ϊ4����m��ֵ��
��3������P��A���������ÿ��3����λ���ȵ��ٶ����յ�C�ƶ�������Qͬʱ��B���������ÿ��2����λ���ٶ����յ�C�ƶ����˶�ʱ��Ϊt�룬��P��Q�����ľ��룿���ú�t�Ĵ���ʽ��ʾ��
![]()
���𰸡���1��8��-18����2��-30��-6����3����0<t��2ʱ�� PQ��2-t ����2<t��![]() ʱ�� PQ=t-2����
ʱ�� PQ=t-2����![]() <t��4ʱ�� PQ��
<t��4ʱ�� PQ��![]() -2t
-2t
��������
��1��������֪��A����B�ľ���Ϊ2�͵�C����B�ľ���Ϊ8������ɣ�
��2����Ϊ�����������O��C�����ʱ����O��C���Ҳ�ʱ�����ÿ�����A��B��C��Ӧ�������������m��
��3����Ϊ�����������P��AB֮��ʱ����P��Q�����B���Ҳ�ʱ����P��Q���ұ�ʱ���г���ʽ���ɣ�
��1����BΪԭ�㣬��C����B�ľ���Ϊ8�����֪��C��Ӧ����Ϊ8������CΪԭ�㣬����֪����A��Ӧ����Ϊ-10����B��Ӧ����Ϊ-8����m=-18���ʴ�Ϊ��8��-18��
��2����O��C���Ҳ�ʱ��
C��Ӧ����Ϊ:��4�� B��Ӧ����Ϊ����12��A��Ӧ����Ϊ����14��
![]()
��O��C�����ʱ��
C��Ӧ����Ϊ:4��B��Ӧ����Ϊ: ��4 �� A��Ӧ����Ϊ:��6��
![]()
��3����0<t��2ʱ
PQ��2t+2-3t=2-t
��2<t��![]() ʱ
ʱ
PQ��3t- (t+2) =t-2
��![]() <t��4ʱ
<t��4ʱ
PQ��![]() -2t
-2t



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С��Ʒ�г�һ��Ӫ�߽�ÿ������Ϊ80Ԫ��ij��С��Ʒԭ����ÿ��100Ԫ���ۣ�һ����۳�100�������������г����飬��������С��Ʒ����ÿ����1Ԫ��������������10����
(1)�þ�Ӫ�߾�Ӫ������Ʒԭ��һ��ɻ�����____Ԫ��
(2)���������С��Ʒÿ������xԪ���þ�Ӫ��һ��ɻ�����yԪ��
�����þ�Ӫ�߾�Ӫ����Ʒһ��Ҫ������2 090Ԫ����ÿ����ƷӦ���۶���Ԫ��
�����y��x֮��ĺ�����ϵʽ���������xȡ��ֵʱ���þ�Ӫ����������������������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
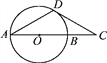
����Ŀ����ͼ��ʾ��D�ǰ뾶ΪR�ġ�O��һ��������D����O�����߽�ֱ��AB���ӳ����ڵ�C�������ĸ���������AD��CD���ڡ�A��30�㣻�ۡ�ADC��120�㣻��DC��![]() R.������ʹ��BC��R����________(�����)��
R.������ʹ��BC��R����________(�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
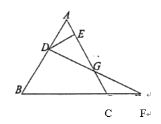
����Ŀ����ͼ���ڱ߳�Ϊ1�ĵȱߡ�ABC�ı�ABȡһ��D������D��DE��AC�ڵ�E����BC�ӳ���ȡһ��F��ʹCF=AD������DF��AC�ڵ�G����EG�ij�Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
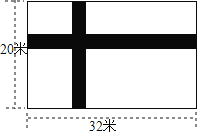
����Ŀ����ͼ��ʾ����Ϊ20�ף���Ϊ32�ij����ε����ϣ���������Ϊx���������ഹֱ��С·�����µIJ�����Ϊ���أ����Ҫ�ڸ��������ϲ�Ƥ��ѡ�ò�Ƥ�ļ۸���ÿƽ��aԪ��
��1�������Ƥ������Ҫ����Ԫ�����ú�a��x��ʽ�ӱ�ʾ��
��2������a��40��x��2ʱ����Ƥ�ķ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90����D��AB���е㣬����A��AE//BC�����D��CD�Ĵ��߽��ڵ�E.
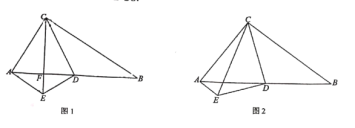
��1����ͼ1����CE��AD�ڵ�F��BC=6����B=30�㣬��AE�ij�
��2����ͼ2����֤AE+CE=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������ǧλ�ϺͰ�λ�ϵ�����֮��Ϊ![]() ��ʮλ�Ϻ�λ�ϵ�����֮��Ϊ
��ʮλ�Ϻ�λ�ϵ�����֮��Ϊ![]() �����
�����![]() ����ô�������λ��Ϊ����ƽ������
����ô�������λ��Ϊ����ƽ������
���磺1423��![]() ��
��![]() ����Ϊ
����Ϊ![]() ������1423������ƽ������
������1423������ƽ������
��1��ֱ��д������С������ƽ��������������������ƽ�������� ����
��2����һ������ƽ�����ĸ�λ����ʮλ�ϵ����ֽ���λ�ã�ͬʱ������λ����ǧλ�ϵ����ֽ���λ�ã��ƽ���ǰ�������������ƽ����Ϊһ������غ�ƽ������
���磺1423��4132Ϊһ�顰��غ�ƽ����
��֤�������һ�顰��غ�ƽ����֮����1111�ı�����
��3�����λ�ϵ�������ǧλ�ϵ����ֵ������Ұ�λ�ϵ�������ʮλ�ϵ�����֮����12�ı�������������ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��������ABCD�ڲ�һ�㣬�ҡ�PAB���������Σ����CPD��_____�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
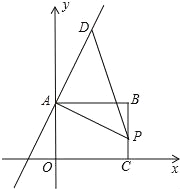
����Ŀ����ͼ������ABC0λ��ֱ������ƽ�棬OΪԭ�㣬A��C�ֱ����������ϣ�B������Ϊ��8��6�����߶�BC����һ����P����֪��D�ڵ�һ���ޣ�
��1��D��ֱ��y��2x+6��һ�㣬����APD�ǵ���ֱ�������Σ����D�����ꣻ
��2��D��ֱ��y��2x��6��һ�㣬����APD�ǵ���ֱ�������Σ����D�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com