
分析 过点P作PD⊥AB于点D,则直角△APD和直角△BPD有公共边PD,在两个直角三角形中,利用三角函数即可用PD表示出AD与BD,根据AB=AD-BD列方程,从而求得PD的长,即为所求.
解答 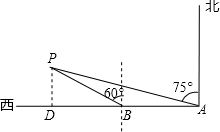 解:如图,过点P作PD⊥AB于点D.
解:如图,过点P作PD⊥AB于点D.
∵在直角△APD中,∠APD=75°,
∴AD=PD•tan75°=(2+$\sqrt{3}$)PD.
∵在直角△BPD中,∠BPD=60°,
∴BD=PD•tan60°=$\sqrt{3}$PD.
∵AB=AD-BD,
∴10=(2+$\sqrt{3}$)PD-$\sqrt{3}$PD,
∴PD=5.
故如果轮船航向不变,那么灯塔P与轮船之间的最近距离是5海里.
点评 本题考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知等腰梯形ABCD中,AD+BC=18cm,sin∠ABC=$\frac{\sqrt{3}}{3}$,AC与BD相交于点O,∠BOC=120°.求AB的长.
已知等腰梯形ABCD中,AD+BC=18cm,sin∠ABC=$\frac{\sqrt{3}}{3}$,AC与BD相交于点O,∠BOC=120°.求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上.
如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com