
【题目】已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.

【答案】(1)130°;(2)120°;(3)互补;(4)∠COB=35°,∠AOD=145°.
【解析】试题分析:(1)根据垂线的定义,可得∠AOB与∠COD的度数,根据余角的定义,可得∠AOC,根据角的和差,可得答案;
(2)根据角的和差,可得答案;
(3)根据角的和差,可得答案;
(4)根据按比例分配,可得答案.
试题解析: (1)由OA⊥OB,OC⊥OD,
得∠AOB=∠COD=90°,
由余角的定义,得∠AOC=∠AOB∠BOC=90°50°=40°,
由角的和差,得∠AOD=∠AOC+∠COD=40°+90°=130°;
(2)由OA⊥OB,OC⊥OD,得∠AOB=∠COD=90°,
由角的和差,得∠AOD=360°∠AOB∠BOC∠COD=360°90°60°90°=120°,
(3)∠AOD+∠BOC=180,
∠AOD+∠BOC=130°+50°=180°;
(4)由角的和差,得∠AOD+∠BOC=360°∠AOB∠COD=180°,
按比例分配,得∠BOC=180°×![]() =35°
=35°
∠AOD=180°×![]() =145°.
=145°.


科目:初中数学 来源: 题型:
【题目】某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论: ⑴小明说:y与x之间的函数关系为y=6.4x+16
⑵小刚说:y与x之间的函数关系为y=8x
⑶小聪说:y与x之间的函数关系在0≤x≤10时,y=8x;在x>10时,y=6.4x+16
⑷小斌说:我认为用下面的列表法也能表示它们之间的关系
购买量/本 | 1 | 2 | 3 | 4 | … | 9 | 10 | 11 | 12 | … |
付款金额/元 | 8 | 16 | 24 | 32 | … | 72 | 80 | 86.4 | 92.8 | … |
⑸小志补充说:如图所示的图象也能表示它们之间的关系.
其中,表示函数关系正确的个数有( )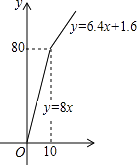
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( )
A.16(1+2x)=25
B.25(1﹣2x)=16
C.16(1+x)2=25
D.25(1﹣x)2=16
查看答案和解析>>
科目:初中数学 来源: 题型:
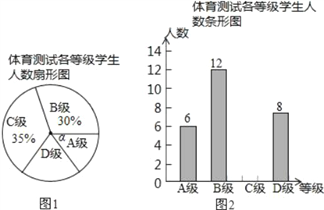
【题目】为了解中考体育科目训练情况,某区从九年级学生中抽取了部分学生进行了一次中考体育科测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(3)该区九年级有学生4000名,如果全部参加这次体育测试,请估计不及格的人数为 ;
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树状图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 到
到![]() 两边的距离相等,且
两边的距离相等,且![]() .
.
(1)先用尺规作出符合要求的点![]() (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设![]() ,
,![]() ,试用
,试用![]() 、
、![]() 的代数式表示
的代数式表示![]() 的周长和面积;
的周长和面积;
(3)设![]() 与
与![]() 交于点
交于点![]() ,试探索当边
,试探索当边![]() 、
、![]() 的长度变化时,
的长度变化时,![]() 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com