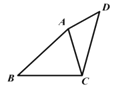
【题目】如图，在四边形 ABCD 中，AC 是对角线，AB=CD，∠DAC+∠BCA=180°，∠BAC+∠ACD=90°，四边形 ABCD 的面积是 18，则 CD 的长是__________.
【答案】6.
【解析】分析: 延长BC至点E,使CE=AD,再连接AE, 证△ACD≌△CAE得
,再证△BAE是等腰直角三角形,得
,最后根据
即可求出CD的长.
详解:如图,延长BC至点E,使CE=AD,再连接AE.
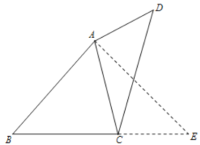
∵∠DAC+∠BCA=180°,
∠ECA+∠BCA=180°
∴∠DAC=∠ECA
在△ACD和△CAE中
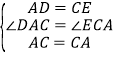
∴△ACD≌△CAE(SAS)
∴∠ACD=∠CAE,CD=AE,
∵∠BAC+∠ACD=90°
∴∠BAC+∠CAE=90°
∴∠BAE=90°
∵AB=CD,CD=AE
∴AB=AE
∴△BAE是等腰直角三角形
∴
∵
,
∴
∵四边形 ABCD 的面积是 18
∴
=18
∵CD>0,
∴CD=6
故答案为:6.
口算心算速算应用题系列答案
同步拓展阅读系列答案科目：初中数学 来源： 题型：
【题目】一个盒子里有完全相同的三个小球，球上分别标上数字-1、1、2．随机摸出一个小球（不放回）其数字记为p，再随机摸出另一个小球其数字记为q，则满足关于x的方程x2+px+q=0有实数根的概率是（ ）.
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，图中有四条互相不平行的直线
、
、
、
所截出的七个角，关于这七个角的度数关系，下列选项正确的是( )
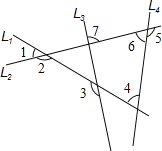
A. ∠2=∠4+∠5 B. ∠3=∠1+∠6 C. ∠1+∠4+∠7=180° D. ∠5=∠1+∠4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠B=∠C，AB=AC=10cm，BC=8cm，点D为AB的中点．
（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC边上相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
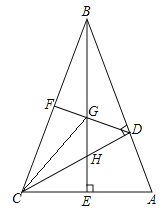
【题目】如图，在△ABC中，∠ABC=45°，CD⊥AB，BE⊥AC，垂足分别为D,E,F为BC中点，BE与DF，DC分别交于点G，H，连接CG，∠ABE=∠CBE.
（1）求证：BH=AC；
（2）若BG=5，GE=4，求线段AE的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进甲、乙两种商品，购进 4 件甲种商品比购进 5 件乙种商品少用 10 元，购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
（1）求甲、乙两种商品每件进价分别是多少元？
（2）若该商店购进甲、乙两种商品共 140 件，都标价 10 元出售，售出一部分降价促销， 以标价的八折售完所有剩余商品，以 10 元售出的商品件数比购进甲种商品件数少 20 件，该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元，求至少购进甲种商品多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小李到某城市行政中心大楼办事，假定乘电梯向上一楼记为+1，向下一楼记为–1．
小李从1楼出发，电梯上下楼层依次记录如下（单位：层）： +5，–3，+10，–8，+12，–6，–10．
（1）请你通过计算说明小李最后是否回到出发点1楼；
（2）该中心大楼每层高2.8m，电梯每上或下1m需要耗电0.1度．根据小李现在所处的位置，请你算一算，当他办事时电梯需要耗电多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝4 cm，BC＝8 cm，点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止．点P，Q的速度的速度都是1 cm/s，连结PQ，AQ，CP，设点P，Q运动的时间为t(s)．
(1)当t为何值时，四边形ABQP是矩形？
(2)当t为何值时，四边形AQCP是菱形？
(3)分别求出(2)中菱形AQCP的周长和面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
