
【题目】如图,在平行四边形ABCD中,E是边AD上一点,CE与BD相交于点O,CE与BA的延长线相交于点G,已知DE=2AE,CE=8.
(1)求GE的长;
(2)若![]() =
=![]() ,
,![]() =
=![]() ,用
,用![]() 、
、![]() 表示
表示![]() ;
;
(3)在图中画出![]()
![]() +
+![]() .(不需要写画法,但需要结论)
.(不需要写画法,但需要结论)

科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.
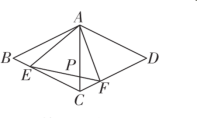
(1)证明:不论E、F在BC、CD上如何运动,总有BE=CF;
(2)当BE=1时,求AP的长;
(3)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,直接写出这个定值;如果变化,是最大值还是最小值?并直接写出最大(或最小)值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
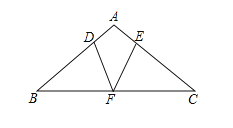
(1)求证:△BDF≌△CEF.
(2)当∠A= 100°,BD=BF时,求∠DFE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
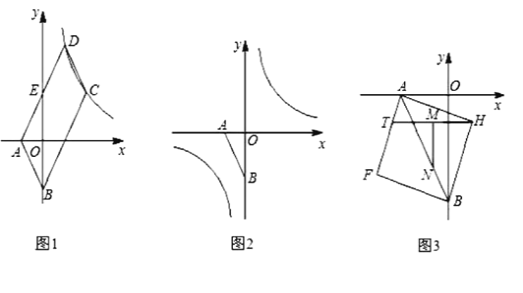
【题目】如图1,已知点![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 两点。
两点。
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图3),点
(如图3),点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明。
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
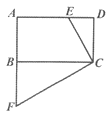
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(﹣2,0),B(1,3).
(1)求抛物线的解析式;
(2)由图象直接写出:x取何值时,y随x的增大而减少;
(3)根据图象回答:x取何值时,y>0.
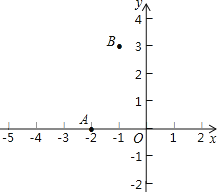
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.
两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
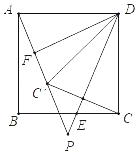
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com