
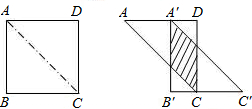
 设平移的距离为x(cm),两个三角形重叠部分(阴影四边形)的面积为S(cm2).
设平移的距离为x(cm),两个三角形重叠部分(阴影四边形)的面积为S(cm2). ?如果存在,请求出此时的平移距离x;如果不存在,请说明理由.
?如果存在,请求出此时的平移距离x;如果不存在,请说明理由. 解:(1)由题意可知△ACD和△A′B′C′都为等腰直角三角形,且AD=2,
解:(1)由题意可知△ACD和△A′B′C′都为等腰直角三角形,且AD=2, (2-x),
(2-x), (2-x)=1:
(2-x)=1: 或x:
或x: (2-x)=
(2-x)= :1,
:1, ,
, 时,重叠部分的四边形的相邻两边之比为1:
时,重叠部分的四边形的相邻两边之比为1: .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
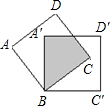 如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个正方形纸片完全重合,按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
| A、30° | B、35° |
| C、45° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
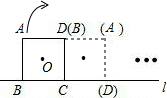 (2012•遵义)如图,将边长为
(2012•遵义)如图,将边长为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为
如图,将边长为2cm的两个互相重合的正方形纸片 按住其中一个不动,另一个纸点B顺时针旋转一个角度,若使重叠部分的面积为4
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com