
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下列结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=![]() .其中正确的结论有 ( )
.其中正确的结论有 ( )

A. 3个 B. 2个 C. 1个 D. 0个
【答案】B
【解析】
①正确.只要证明∠EAC=∠ACB,∠ABC=∠AFE=90°即可;
②正确.由AD∥BC,推出△AEF∽△CBF,推出![]() ,由AE=
,由AE=![]() AD=
AD=![]() BC,推出
BC,推出![]() =
=![]() ,即CF=2AF;
,即CF=2AF;
④错误,设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有![]() ,即b=
,即b=![]() a,可得tan∠CAD=
a,可得tan∠CAD=![]() =
=![]() 即可得.
即可得.
如图,过D作DM∥BE交AC于N,
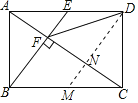
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
∴CF=2AF,故②正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有
![]() ,即b=
,即b=![]() a,
a,
∴tan∠CAD=![]() =
=![]() =
=![]() ,故③错误,
,故③错误,
所以正确的有2个,
故选B.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10![]() km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4![]() km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.

A.8![]() B.9
B.9![]() C.6
C.6![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-5,1),B(-1,1),C(-4,3).
(1)若△A1B1C1与△ABC关于y轴对称,点A,B,C的对应点分别为A1,B1,C1,请画出△A1B1C1并写出A1,B1,C1的坐标;
(2)若点P为平面内不与C重合的一点,△PAB与△ABC全等,请写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍![]() 购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
![]() 求购买1副乒乓球拍和1副羽毛球拍各需多少元;
求购买1副乒乓球拍和1副羽毛球拍各需多少元;
![]() 若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com