
【题目】如图,∠OAB=45°,点A的坐标是(4,0),AB= ![]() ,连结OB.
,连结OB.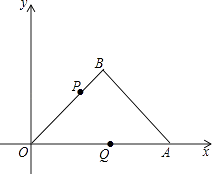
(1)直接写出点B的坐标.
(2)动点P从点O出发,沿折线O﹣B﹣A方向向终点A匀速运动,另一动点Q从点O出发,沿OA方向匀速运动,若点P的运动速度为 ![]() 个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
(3)动点P仍按(2)中的方向和速度运动,但Q点从A点向O点运动,速度为1个单位/秒,P、Q与△OAB中的任意一个顶点形成直角三角形时,求此时t(t≠0)的值.
【答案】
(1)
解:过B作BC⊥OA于C,
∵∠OAB=45°,
∴△ACB为等腰直角三角形,
∵AB=2 ![]() ,
,
∴BC=AC=2,
∵A(4,0),
∴OA=4,
∴OC=OA﹣AC=4﹣2=2,
∴B(2,2)
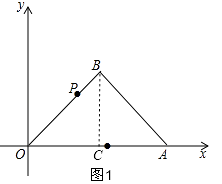
(2)
解:过P作PD⊥OA于D,
如图1,由(1)得:OC=BC=2,∠BCO=90°,
∴∠AOB=45°,
如图2,由题意得:OP= ![]() t,OQ=t,
t,OQ=t,
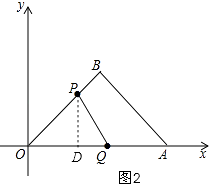
∵△POD是等腰直角三角形,
∴PD= ![]() =t,
=t,
∵S△OPQ=1.5,
∴ ![]() OQPD=1.5,
OQPD=1.5,
![]() t2=1.5,
t2=1.5,
t= ![]() ,
,
答:当t= ![]() 时,△OPQ的面积等于1.5
时,△OPQ的面积等于1.5
(3)
解:分四种情况:
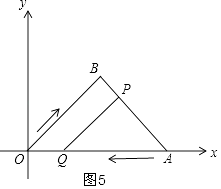
①0<t≤2时,∠OPQ=90°,如图3,

由题意得:OP= ![]() t,AQ=t,OQ=4﹣t,
t,AQ=t,OQ=4﹣t,
则cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t= ![]() ;
;
②当0<t≤2时,∠OQP=90°,如图4,
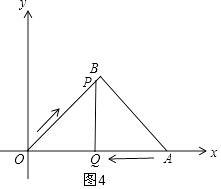
由题意得:OP= ![]() t,AQ=t,OQ=4﹣t,
t,AQ=t,OQ=4﹣t,
则cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t=2;
③当2<t<4时,AQ=t,AP=4 ![]() ﹣
﹣ ![]() t,
t,
当∠APQ=90°时,如图5,
cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t= ![]() ;
;
④如图6,点Q与O重合,点P与A重合,
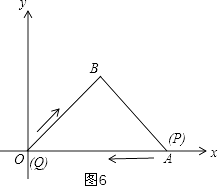
∠PBQ=90°,此时t=4;
综上所述,P、Q与△OAB中的任意一个顶点形成直角三角形时,t的值为 ![]() 或2或
或2或 ![]() 或4.
或4.
【解析】(1)如图1,过B作BC⊥OA于C,根据∠OAB=45°,可知△ACB为等腰直角三角形,求出BC和AC的长为2,再由点A的坐标得出OA=4,所以得出B(2,2);(2)如图2,作△OPQ的高线PD,根据速度和时间表示动点的路程:OP= ![]() t,OQ=t,根据图1求出∠AOB=45°,所以△POD是等腰直角三角形,表示出高线PD的长,代入面积公式列等量关系式可求得结论;(3)分四种情况进行讨论:①当0<t≤2时,∠OPQ=90°,如图3,②当0<t≤2时,∠OQP=90°,如图4,③当2<t<4时,∠APQ=90°,如图5,④点Q与O重合,点P与A重合,如图6;分别根据45°的余弦列式求出.
t,OQ=t,根据图1求出∠AOB=45°,所以△POD是等腰直角三角形,表示出高线PD的长,代入面积公式列等量关系式可求得结论;(3)分四种情况进行讨论:①当0<t≤2时,∠OPQ=90°,如图3,②当0<t≤2时,∠OQP=90°,如图4,③当2<t<4时,∠APQ=90°,如图5,④点Q与O重合,点P与A重合,如图6;分别根据45°的余弦列式求出.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
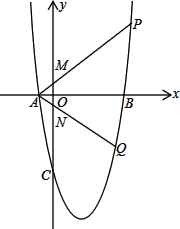
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数. 解:因为∠1=∠2=80°(已知),
所以AB∥CD()
所以∠BGF+∠3=180°()
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD= . (等式性质).
因为FG平分∠EFD(已知).
所以∠3=∠EFD(角平分线的性质).
所以∠3= . (等式性质).
所以∠BGF= . (等式性质).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数. 小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.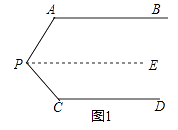
(1)按小明的思路,易求得∠APC的度数为度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由; 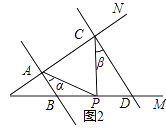
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a、b、c的值为( )
A.1、2、-15
B.1、-2、-15
C.-1、-2、-15
D.-1、2、-15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com