
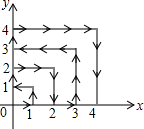
 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5). 分析 根据跳蚤跳到正方形右顶点位置用时规律及下一步方向知第30秒时跳蚤位于(5,5)位置,下一步向左跳动,进而知第35秒的坐标.
解答 解:跳蚤跳到(1,1)位置用时1×2=2秒,下一步向左跳动;
跳到(2,2)位置用时2×3=6秒,下一步向下跳动;
跳到(3,3)位置用时3×4=12秒,下一步向左跳动;
跳到(4,4)位置用时4×5=20秒,下一步向下跳动;
…
由以上规律可知,跳蚤跳到(n,n)位置用时n(n+1)秒,
当n为奇数时,下一步向左跳动;
当n为偶数时,下一步向下跳动;
∴第5×6=30秒时跳蚤位于(5,5)位置,下一步向左跳动,
则第35秒时,跳蚤需从(5,5)向左跳动5个单位到(0,5),
故答案为:(0,5).
点评 本题主要考查点的坐标问题,解决本题的关键是读懂题意,能够正确确定点运动的规律,从而可以得到到达每个点所用的时间.


科目:初中数学 来源: 题型:解答题
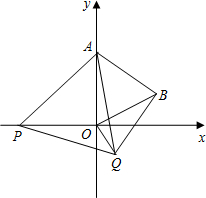 在平面直角坐标系中如图,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其右侧作等边三角形APQ,当点P运动到原点O处时,记Q的位置为B,已知在直角三角形中两直角边的平方和等于斜边的平方,即直角三角形两直角边长为a,b,斜边长为c,则a2+b2=c2.
在平面直角坐标系中如图,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其右侧作等边三角形APQ,当点P运动到原点O处时,记Q的位置为B,已知在直角三角形中两直角边的平方和等于斜边的平方,即直角三角形两直角边长为a,b,斜边长为c,则a2+b2=c2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com