
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

【答案】CD,同旁内角互补两直线平行,∠APC,两直线平行内错角相等,∠BAP,∠APC,∠4,内错角相等两直线平行,两直线平行内错角相等
【解析】根据平行线的性质和判定即可解决问题;
∵![]() ,(已知)
,(已知)
∴AB∥CD.(同旁内角互补两直线平行)
∴∠BAP=∠APC.(两直线平行,内错角相等)
又∵∠1=∠2,(已知)
∠3=∠BAP∠1,
∠4=∠APC∠2,
∴∠3=∠4(等式的性质)
∴AE∥PF.(内错角相等两直线平行)
∴∠E=∠F.(两直线平行内错角相等)
故答案为CD,同旁内角互补两直线平行,∠APC,两直线平行内错角相等,∠BAP,∠APC,∠4,内错角相等两直线平行,两直线平行内错角相等;


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a,b是关于x的一元二次方程![]() 的两个根,则Rt△ABC中较短的直角边长为__________.
的两个根,则Rt△ABC中较短的直角边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(﹣a3)2+a6=_____.
(2)2a5b(﹣ab)3=_____.
(3)![]() =_____.
=_____.
(4)(﹣a)3(﹣a)4=_____.
(5)(x+2)(x﹣3)=_____.
(6)(2×103)×(5×104)=_____.(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
已知:等边三角形ABC
(1)如图1,P为等边△ABC外一点,且∠BPC=120°.试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
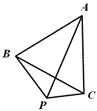
(2)如图2,P为等边△ABC内一点,且∠APD=120°.求证:PA+PD+PC>BD
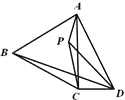
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC=12,BD=8,则经过________秒后,四边形BEDF是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
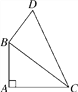
【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).

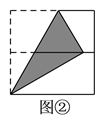


A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下
的中点.以下![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() .正确的是( )
.正确的是( )
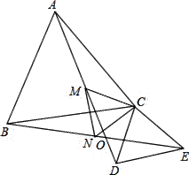
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com