
【题目】如图,四边形ABCD内接于⊙O,BC=CD,∠C=2∠BAD.
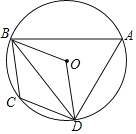
(1)求∠BOD的度数;
(2)求证:四边形OBCD是菱形;
(3)若⊙O的半径为r,∠ODA=45°,求△ABD的面积(用含r的代数式表示).
【答案】(1)120°;(2)证明见解析;(3)(1+![]() )r2.
)r2.
【解析】
(1)结合圆的内接四边形对角互补,运用方程思想,再运用圆周角定理求解即可;
(2)连接OC,证明△BOC和△DOC都是等边三角形,进而即可证明结论;
(3)分别计算△BOD,△AOD和△AOB的面积,再求和即可.
(1)∵四边形ABCD内接于⊙O,
∴∠C+∠BAD=180°,
∵∠C=2∠BAD,
∴∠C=120°,∠BAD=60°,
∴∠BOD=2∠BAD=120°;
(2)如图1连接OC,
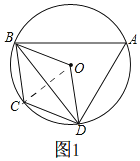
∵BC=CD,
∴∠BOC=∠DOC=60°,
∵OB=OC=OD,
∴△BOC和△DOC都是等边三角形,
∴OB=OC=OD=BC=DC,
∴四边形OBCD是菱形,
(3)如图2,连接OA,过点A作BO的垂线交BO的延长线于点N,
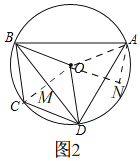
∵∠BOD=120°,OB=OD,
∴∠ODM=30°,
∵∠BOM=∠DOM,
∴OM⊥BD,
∴OM=![]() r,DM=
r,DM=![]() r,
r,
∴BD=2DM=![]() r,
r,
∴S△BOD=![]() r2,
r2,
∵∠ODA=45°,OA=OD,
∴∠OAD=∠ODA=45°,
∴∠AOD=90°,
∴S△AOD=![]() r2,
r2,
∵∠BOD=120°,∠AOD=90°,
∴∠AOB=150°,
∴∠AON=30°,
∴AN=![]() OA=
OA=![]() r,
r,
∴S△AOB=![]() r2,
r2,
∴△ABD的面积为![]() r2+
r2+![]() r2+
r2+![]() r2=(1+
r2=(1+![]() )r2.
)r2.


科目:初中数学 来源: 题型:
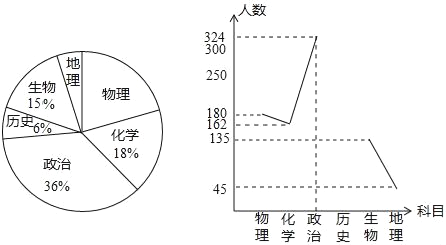
【题目】某校对九年级学生进行随机抽样调查,被抽到的学生从物理、化学、生物、地理、历史和政治这六科中选出自己最喜欢的科目,将调查数据汇总整理后,绘制了两幅不同的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?求出地理学科所在扇形的圆心角;
(2)将折线统计图补充完整;
(3)若该校九年级学生约2000人请你估算喜欢物理学科的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为20元的商品,经调研,当该商品每件售价为30元时,每天可销售200件:当每件的售价每增加1元,每天的销量将减少5件.
![]() 求销量
求销量![]() 件
件![]() 与售价
与售价![]() 元
元![]() 之间的函数表达式;
之间的函数表达式;
![]() 如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?
如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?
![]() 该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.
该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
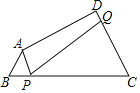
【题目】我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.
概念理解:在“矩形、菱形和正方形”这三种特殊四边形中,不一定是“等邻角四边形”的是______.
问题探究:如图,在等邻角四边形ABCD中,∠B=∠C,AB=3,BC=9,P为线段BC上一动点(不包含端点B,C),Q为直线CD上一动点,连结PA,PQ,在P,Q的运动过程中始终满足∠APQ=∠B,当CQ达到最大时,试求此时BP的长.
应用拓展:在以60°为等角的等邻角四边形ABCD中,∠D=90°,若AB=3,AD=![]() ,试求等邻角四边形ABCD的周长.
,试求等邻角四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
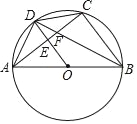
【题目】如图,AB是⊙O的直径,点C是圆上任意一点,点D是AC中点,OD交AC于点E,BD交AC于点F,若BF=1.25DF,则tan∠ABD的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
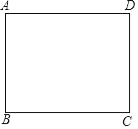
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
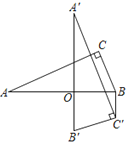
【题目】如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕AB上的点O顺时针旋转90°,得到△A'B'C',连结BC'.若BC'∥A'B',则OB的值为( )
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
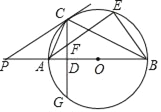
【题目】如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D
(1)求证:PC是⊙O的切线;
(2)求证:![]() ;
;
(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
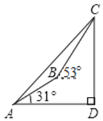
【题目】鄂州市电信部门积极支持鄂州国际航空大都市的建设,如图,计划修建一条连接B,C两地的电缆,测量人员在山脚A测得B,C两地的仰角分别为31°和45°,在B处测得C处的仰角为53°.已知C地比A地髙50m,则电缆BC至少需要多少米?(精确到1m,参考数据:sin31°≈![]() ,tan31°≈
,tan31°≈![]() ,sin37°≈0.6,cos37°≈0.8)
,sin37°≈0.6,cos37°≈0.8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com