
【题目】若数a使关于x的不等式组 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
科目:初中数学 来源: 题型:
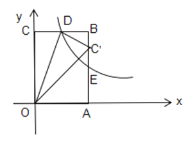
【题目】如图,平面直角坐标系中,矩形ABCD与双曲线![]() 交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
A. 4B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,在矩形ABCD中,点E在BC边上,△AEF=90°
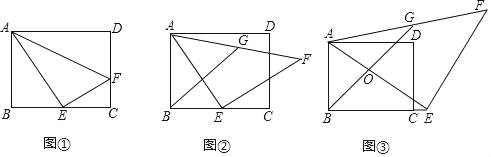
(1)如图①,已知点F在CD边上,AD=AE=5,AB=4,求DF的长;
(2)如图②,已知AE=EF,G为AF的中点,试探究线段AB,BE,BG的数量关系;
(3)如图③,点E在矩形ABCD的BC边的延长线上,AE与BG相交于O点,其他条件与(2)保持不变,AD=5,AB=4,CE=1,求△AOG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为A、B、C、D四个等次,绘制成如图所示的不完整的统计图,请你依图解答下列问题:
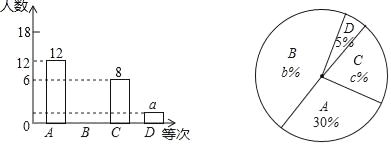
(1)a= ,b= ,c═ ,
(2)请将条形统计图补充完整,并计算表示C等次的扇形所对的圆心角的度数为= ,
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1+y2,其中y1与x成反比例,y2与x﹣2成正比例,函数的自变量x的取值范围是x≥![]() ,且当x=1或x=4时,y的值均为
,且当x=1或x=4时,y的值均为![]() .
.
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探究:
①根据解析式,补全下表:
x |
| 1 |
| 2 |
| 3 | 4 | 6 | 8 | … |
y |
|
|
|
|
|
|
| … |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.

(3)结合画出的函数图象,解决问题:
①当x=![]() ,
,![]() ,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
②若直线y=k与该函数图象有两个交点,则k的取值范围是 ,此时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
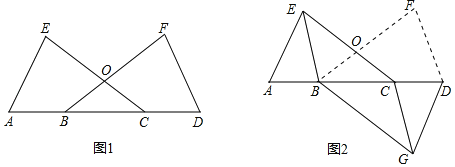
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com