
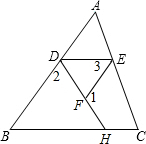
 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.分析 首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.
解答 解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴∠EFD=∠2(同角的补角相等)①
∴AB∥EF(内错角相等,两直线平行)②
∴∠ADE=∠3(两直线平行,内错角相等)③
∵∠3=∠B(已知)④
∴∠ADE=∠B(等量代换)⑤
∴DE∥BC(同位角相等,两直线平行)⑥
∴∠AED=∠C(两直线平行,同位角相等)⑦.
故答案为:∠EFD=∠2;AB∥EF;两直线平行,内错角相等;已知;∠ADE=∠B;同位角相等,两直线平行;两直线平行,同位角相等.
点评 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.
如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.| A. | 12 | B. | 18 | C. | 22 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
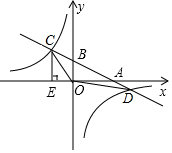 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票张数 | 1~50张 | 51~100张 | 100张以上 |
| 每张票价格 | 10元 | 8元 | 6元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com