
【题目】在有理数2、3、-4、-5、6中,任取两个数相乘所得积最大是 .
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知四个命题: ①若一个数的相反数等于它本身,则这个数是0;
②若一个数的倒数等于它本身,则这个数是1;
③若a=b,则a2=b2;
④若一个数的绝对值就等于它本身,则这个数是正数.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在5×6的方格图中
在图1中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分)
在图2中,将线段A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分)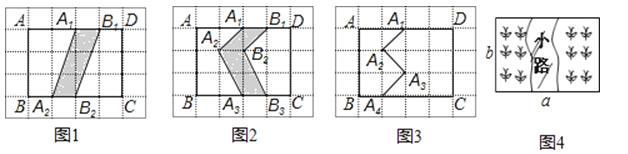
(1)在图3中,画出将折线A1A2A3A4向右平移1单位后的图形,并用阴影画出由这两条折线所围成的封闭图形.
(2)设上述三个图形中,矩形ABCD分别除去阴影部分后剩余部分的面积记为S1、S2、S3 , 则S1= ,S2= S3=
(3)如图4,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想草地部分的面积是 .(用含a、b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
A.0.35×1010元
B.3.5×108元
C.3.5×109元
D.35×108元
查看答案和解析>>
科目:初中数学 来源: 题型:
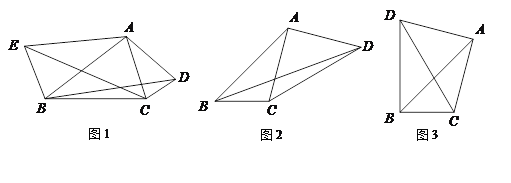
【题目】【问题探究】
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD= 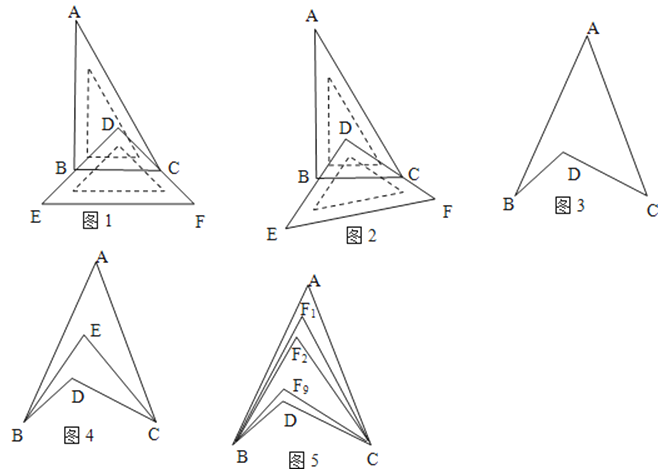
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着 关系
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,∠BEC
②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛实验中,甲、乙两根蜡烛燃烧时剩余部分的高度![]() (cm)与燃烧时间
(cm)与燃烧时间![]() (h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:

(1)甲乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求出甲、乙两根蜡烛燃烧时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com