
【题目】计算题|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(1)计算:|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(2)解不等式组 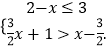 并求其最小整数解.
并求其最小整数解.
【答案】
(1)解:原式= ![]() ﹣1﹣2
﹣1﹣2 ![]() +
+ ![]() ﹣1
﹣1
=﹣2
(2)解: 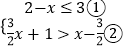
解不等式①得x≥﹣1;
解不等式②得x>﹣5;
不等式组的解集为x≥﹣1;
最小整数解为﹣1
【解析】(1)根据绝对值,特殊角的锐角三角函数值,零指数的意义,二次根式的化简分别进行化简,再按实数的运算方法进行计算即可;(2)解不等式①得x≥﹣1;解不等式②得x>﹣5;然后根据同大取大得出解集,在解集范围内得出最小整数解为﹣1。
【考点精析】解答此题的关键在于理解二次根式的性质与化简的相关知识,掌握1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来,以及对绝对值的理解,了解正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.


科目:初中数学 来源: 题型:
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, ![]() =1.732,
=1.732, ![]() =1.414)
=1.414)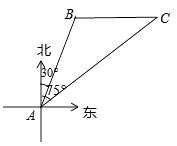
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅,1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅,1个小餐厅分别可供多少名 就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个有理数a,b满足a+b=ab,则称a,b互为特征数.
(1)3与 互为特征数;
(2)正整数n (n>1)的特征数为 ;(用含n的式子表示)
(3)若m,n互为特征数,且m+mn=-2,n+mn=3,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.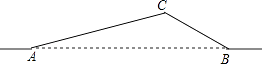
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
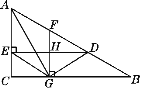
【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判断四边形AEGF是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
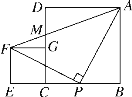
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com