
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.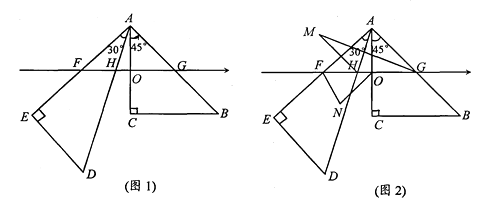
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 , 点H对应的数轴上的数是;
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.
【答案】
(1)-5;-1
(2)解:∵∠AHF的平分线和∠AGH的平分线交于点M,
∴2∠FHM=![]() ∠FHA,2∠HGM=
∠FHA,2∠HGM=![]() ∠HGA,
∠HGA,
∵∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,
∴2∠M+2∠HGM=∠HGA+∠HAG,
∴∠M=![]()
![]() ∠HAG=
∠HAG=![]()
![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]()
![]() ɑ+22.5
ɑ+22.5
(3)解: ∵∠EFH的平分线和∠FOC的平分线交于点N,
∴∠N=90°-![]()
![]() ∠FAO=90°-
∠FAO=90°-![]()
![]() ∠FAH-
∠FAH-![]()
![]() ∠OAH (可以直接利用∠N=90°-
∠OAH (可以直接利用∠N=90°-![]()
![]() ∠FAO)
∠FAO)
=90°-15°- ![]() ∠OAH
∠OAH
=75°- ![]() ∠OAH,
∠OAH,
∵∠M=![]()
![]() ∠OAH+22.5°,
∠OAH+22.5°,
∴∠M+∠N=97.5°.
【解析】解:(1)如图1,∵AC的中点过数轴的原点O,AC=8,
∴AO=4,
∵△AGH的面积是10,
∴![]() ×4×GH=10,
×4×GH=10,
解得GH=5,
又∵∠AOG=90,∠OAG=45,
∴OG=OA=4,
∴OH=1,
∴点H对应的数轴上的数是1,
∵△AHF的面积是8,
∴![]() FH4=8,
FH4=8,
解得FH=4,
∴OF=OH+FH=5,
∴点F对应的数轴上的数是5,
故答案为:5,1;
(1)根据中点的定义得出OA=4,根据三角形的面积得出![]() ×4×GH=10,从而得出GH的长度,根据等腰直角三角形的性质得出OG=OA=4,从而得出OH的长,得到点H对应的数轴上的数是1,再根据三角形的面积得出
×4×GH=10,从而得出GH的长度,根据等腰直角三角形的性质得出OG=OA=4,从而得出OH的长,得到点H对应的数轴上的数是1,再根据三角形的面积得出![]() FH4=8,从而得出FH的长,根据OF=OH+FH,得出OF的长,从而得出点F对应的数轴上的数是5;
FH4=8,从而得出FH的长,根据OF=OH+FH,得出OF的长,从而得出点F对应的数轴上的数是5;
(2)根据角平分线的定义得出2∠FHM= ∠FHA,2∠HGM= ∠HGA,根据三角形的外角定理得出∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,根据等量代换得出2∠M+2∠HGM=∠HGA+∠HAG,根据等式的性质从而得出答案∠M=![]() ∠HAG=
∠HAG=![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]() ɑ+22.5 ;
ɑ+22.5 ;
(3)直接利用结论∠N=90°-![]() ∠FAO=75°-
∠FAO=75°-![]() ∠OAH,又因∠M=
∠OAH,又因∠M=![]() ∠OAH+22.5°,从而得出∠M+∠N=97.5°.
∠OAH+22.5°,从而得出∠M+∠N=97.5°.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点A、B,抛物线
轴分别交于点A、B,抛物线![]() 经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
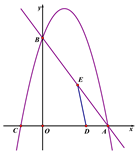
(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣2,y1),(﹣4,y,2)在函数y=x2﹣4x+7的图象上,那么y1 , y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同号两数相乘,取原来的符号
B.一个数与﹣1相乘,积为该数的相反数
C.一个数与0相乘仍得这个数
D.两个数相乘,积大于任何一个乘数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向左平移1个单位,则平移后的二次函数的解析式为( )
A.y=x2﹣1B.y=x2+1C.y=(x﹣1)2D.y=(x+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 斜边相等的两个直角三角形全等 B. 腰相等的两个等腰三角形全等
C. 有一边相等的等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是正方形,
是正方形, ![]() 是
是 ![]() 垂直平分线上的点,点
垂直平分线上的点,点 ![]() 关于
关于 ![]() 的对称点是
的对称点是 ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() .
.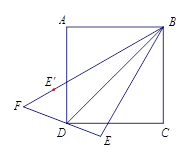
(1)若点 ![]() 是
是 ![]() 边的中点,连接
边的中点,连接 ![]() ,则
,则 ![]() =;
=;
(2)小明从老师那里了解到,只要点 ![]() 不在正方形的中心,则直线
不在正方形的中心,则直线 ![]() 与
与 ![]() 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 ![]() 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.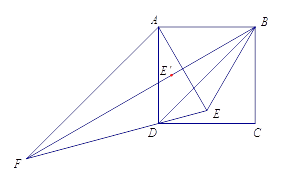
如图,将点 ![]() 选在正方形内,且△
选在正方形内,且△ ![]() 为等边三角形,求出直线
为等边三角形,求出直线 ![]() 与
与 ![]() 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线 ![]() 与
与 ![]() 所夹锐角度数的思路.
所夹锐角度数的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c为平面上三条不同直线,
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b⊥c,则a与c的位置关系是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com