
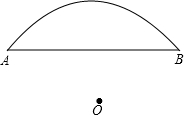
 如图,某座桥的桥拱是圆弧形,O为其圆心,它的跨度AB为8米,拱高为2米,求桥拱的半径.
如图,某座桥的桥拱是圆弧形,O为其圆心,它的跨度AB为8米,拱高为2米,求桥拱的半径. 分析 设圆的半径为R米,由于CD平分弧AB,且CD⊥AB,根据垂径定理的推论得到圆心O在CD的延长线上,再根据垂径定理得到CD平分AB,则AD=$\frac{1}{2}$AB=4,在Rt△OAD中,利用勾股定理可计算出半径R.
解答 解:如图,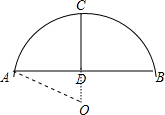 设圆的半径为R米,
设圆的半径为R米,
∵CD平分弧AB,且CD⊥AB,
∴圆心O在CD的延长线上,
∴CD平分AB,
∴AD=$\frac{1}{2}$AB=4,
连OA,
在Rt△OAD中,AD=4,OA=R,OD=R-CD=R-2,
∵OA2=OD2+AD2,
∴R2=42+(R-2)2,
解得R=$\sqrt{5}$,
即拱桥所在圆的半径$\sqrt{5}$米.
点评 本题考查了垂径定理的应用:先把实际问题中的数据与几何图形中的量对应起来,然后根据垂径定理及其推论进行证明或计算.


科目:初中数学 来源: 题型:解答题
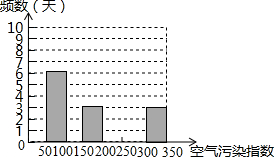 根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.
根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.| 空气污染指数 | 频数(天) | 频率 |
| 50<x≤100 | 6 | 0.2 |
| 100<x≤150 | a | 0.3 |
| 150<x≤200 | 3 | 0.1 |
| 200<x≤250 | 6 | 0.2 |
| 250<x≤300 | b | c |
| 300<x≤350 | 3 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
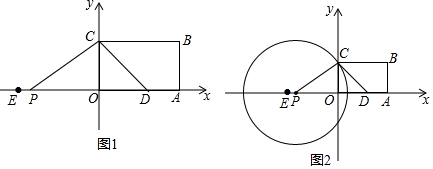
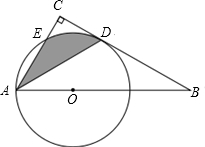 如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com