
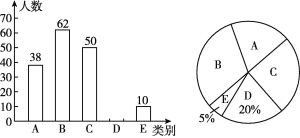
����Ŀ��ijƷ��ţ�̹�Ӧ���ṩA��B��C��D��E���ֲ�ͬ��ζ��ţ�̹�ѧ��ѡ��ijУΪ���˽�ѧ���Բ�ͬ��ζ��ţ�̵�ϲ�ã���ȫУ��ţ�̵�ѧ��������������飬�����ݵ�������������ͼ��ʾ������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ������������⣺
(1)���ε����ѧ���ж�������
(2)��ȫ����ͳ��ͼ���������ϲ��C��ζţ�̵�ѧ��������Ӧ������Բ�ĽǵĶ�����
(3)��У����1 200��ѧ�����˸�Ʒ�Ƶ�ţ�̣�ţ�̹�Ӧ��ÿ��ֻΪÿ����ţ�̵�ѧ������һ��ţ�̣�Ҫʹѧ��ÿ�춼�ܺȵ��Լ�ϲ�õ�Ʒζ��ţ�̣�ţ�̹�Ӧ��ÿ��������У��ţ���У�B��ζţ��Ҫ��C��ζţ��Լ���Ͷ��ٺУ�
���𰸡���1��200����2����������ͼ��������90�㣻��3��72.
��������
��1������ϲ��E��ζ��ţ�̵�ѧ����������ռ�İٷֱȣ�����������ε����ѧ������
��2���õ������������ȥA��B��C��E����ϲ�ò�ͬ��ζ��ţ�̵����������ϲ��D��ζ��ţ����������ȫͳ��ͼ������360������ϲ��C��ζ��ţ�̵�ѧ��������ռ�İٷֱȣ��������ϲ��C��ζ��ţ�̵�ѧ������������ͳ��ͼ�е�Բ�ĽǵĶ�����
��3����B��ζ��ţ�̺�����ȥC��ζţ�̺������ɣ�
�⣺(1)���ε����ѧ����10��5%��200(��)��
(2)ϲ��D��ζţ�̵�ѧ����200��20%��40(��)����ȫ����ͳ��ͼ��ͼ��

ϲ��C��ζţ�̵�ѧ��������Ӧ������Բ�ĽǵĶ���Ϊ360���![]() ��90��.
��90��.
(3)�������⣬��1 200��![]() ��1 200��
��1 200��![]() ��72(��)��
��72(��)��
��B��ζţ��Ҫ��C��ζţ��Լ����72�У�


 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳���
�ı߳���![]() ��
��![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ������
������![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����Сֵ��_______.
����Сֵ��_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
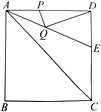
����Ŀ����ͼ��������L��y=ax2+bx+c��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��
��1����������L�Ľ���ʽ��
��2����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ���������OBC�ڣ�������OBC�ı߽磩����h��ȡֵ��Χ��
��3�����P��������L����һ�㣬��Q��ֱ��l��x=��3�ϣ���PBQ�ܷ��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����ܣ�������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��m��4���ڷ���������y=![]() ��ͼ���ϣ�������������ͼ����P�͵�Q��6��n����
��ͼ���ϣ�������������ͼ����P�͵�Q��6��n����
��1���������������Ľ���ʽ��
��2����x������һ��M��ʹ��MPQ���������18��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����A��B��C������ͬһֱ���ϣ����߶�AB=6 cm��BC=4 cm����M��N�ֱ�ΪAB��BC���е㣬��ôM��N����֮��ľ���Ϊ( )
A. 5 cm B. 1 cm C. 5��1 cm D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
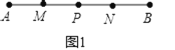
����Ŀ����ͼ����P���߶�AB�ϵ�һ�㣬��M��N�ֱ����߶�AP��PB���е㣮
��1����ͼ1������P���߶�AB���е㣬��MP=4cm�����߶�AB�ij���
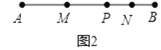
��2����ͼ2������P���߶�AB�ϵ���һ�㣬��AB=12cm�����߶�MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �Ķ����в��ϣ�����֪��
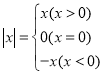
�������ǿ�������������������о���ֵ�Ĵ���ʽ���绯�����ʽ![]() ʱ����
ʱ����![]() �����
�����![]() ����
����![]() �����
�����![]() ����-1��2�ֱ�Ϊ
����-1��2�ֱ�Ϊ![]() ��
��![]() �����ֵ��.����������Χ�ڣ����ֵ-1��2�ɽ�ȫ���������ֳɲ��ظ��Ҳ���©������3�������
�����ֵ��.����������Χ�ڣ����ֵ-1��2�ɽ�ȫ���������ֳɲ��ظ��Ҳ���©������3�������
�ٵ�![]() ʱ��ԭʽ
ʱ��ԭʽ![]() ��
��
�ڵ�![]() ʱ��ԭʽ
ʱ��ԭʽ![]() ��
��
�۵�![]() ʱ��ԭʽ
ʱ��ԭʽ![]() .
.
����������
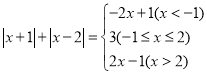
ͨ�������Ķ��������������ʣ�
(1)�ֱ����![]() ��
��![]() �����ֵ��
�����ֵ��
(2)�������ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���һ����ʽ�ܻ���һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽ����������ʽΪ����г��ʽ�����磺![]() ����
����![]() ������г��ʽ����
������г��ʽ����
(1)���з�ʽ�У���������г��ʽ������_____(�����)��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��
(2)������г��ʽ��![]() ����һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽΪ��
����һ����ʽ��һ������Ϊ�����ķ�ʽ�ĺ͵���ʽΪ��![]() ��_______(Ҫд�����ι���)��
��_______(Ҫд�����ι���)��
(3)Ӧ�ã��Ȼ���![]() ������xȡʲô����ʱ����ʽ��ֵΪ������
������xȡʲô����ʱ����ʽ��ֵΪ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
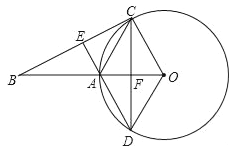
����Ŀ����ͼ����O�İ뾶Ϊ6cm��������O��һ��C����O�����߽��뾶OA���ӳ��ڵ�B������ACO��ƽ���߽���O�ڵ�D����OA�ڵ�F���ӳ�DA��BC�ڵ�E��
��1����֤��AC��OD��
��2�����DE��BC����AC�ij�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com