
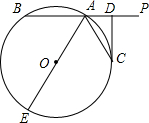
 如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.
如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.分析 (1)连接OC,根据OA=OC推出∠OCA=∠OAC,根据角平分线得出∠OCA=∠OAC=∠CAP,推出OC∥AP,得出OC⊥CD,根据切线的判定推出即可;
(2)过O作OM⊥AB于M,得出矩形OMDC,推出OM=CD,OC=AM+AD,设AD=x,则DC=OM=2x,AM=DM-DA=5-x,得出方程52=(5-x)2+(2x)2,求出x的值即可求出AB的长.
解答 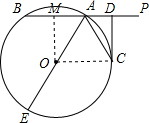 (1)证明:连接OC.
(1)证明:连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵AC平分∠PAE,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线.
(2)解:过O作OM⊥AB于M.
即∠OMA=90°,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD.
∵CD=2AD,
∴设AD=x,则DC=OM=2x,AM=DM-DA=5-x,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴52=(5-x)2+(2x)2,
解得 x1=0(不合题意,舍去),x2=2.
则 AM=DM-DA=5-x=3,
∵OM⊥AB,
∴AB=2AM=6.
点评 本题考查了矩形的性质和判定,勾股定理、垂径定理、切线的判定、平行线的性质和判定等知识点,主要考查学生综合运用定理进行推理的能力,用了方程思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.
如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
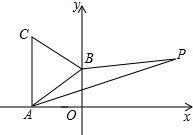 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
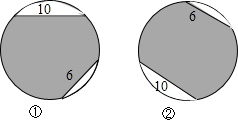 在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )
在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )| A. | S①>S② | B. | S①<S② | C. | S①=S② | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
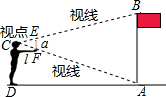 小明把手臂水平向前伸直,手持长为a的小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使站在点D处正好看到旗杆的底部和顶部,如果小明的手臂长为l=40cm,小尺的长a=20cm,点D到旗杆底部的距离AD=40m,求旗杆的高度.
小明把手臂水平向前伸直,手持长为a的小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使站在点D处正好看到旗杆的底部和顶部,如果小明的手臂长为l=40cm,小尺的长a=20cm,点D到旗杆底部的距离AD=40m,求旗杆的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com