
分析 (1)本题涉及零指数幂、立方根、绝对值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)通分后相加,然后因式分解,再相除.
解答 解:(1)原式=3+$\sqrt{2}$-1-2-1
=$\sqrt{2}$-1;
(2)原式=$\frac{{x}^{2}+1}{x-2}$+$\frac{3-4x}{x-2}$
=$\frac{{x}^{2}-4x+4}{x-2}$
=$\frac{(x-2)^{2}}{x-2}$
=x-2.
点评 (1)本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是掌握零指数幂、立方根、绝对值、二次根式化简等考点的运算.
(2)本题考查了分式的加减运算,熟悉通分和因式分解是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
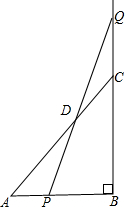 等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.
等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com