
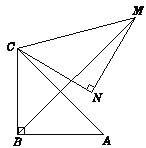
【题目】如图,在Rt△ABC中,∠ABC=90°, AB=BC=![]()
![]() .将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,BN,求BM的长.(提示: 连接BN,先证:AC⊥BM.再利用含30°的直角三角形的性质解答)
.将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,BN,求BM的长.(提示: 连接BN,先证:AC⊥BM.再利用含30°的直角三角形的性质解答)
【答案】BM的长为![]() .
.
【解析】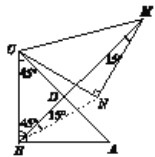 解析:连接BN,设CA与BM相交于点D(如图所示),
解析:连接BN,设CA与BM相交于点D(如图所示),
由题意易得△BCN为等边三角形,.......................(1分)
所以BN=NC=NM,∠BNM=60°+90°=150°,................(3分)
所以∠NBM=∠NMB=15°,...............................................(4分)
所以∠CBM=60°-15°=45°................................................(5分)
∠CMB=45°-15°=30°................................................(6分)
又因为∠BCA=45°,所以∠CDB=90°........................................(7分)
所以△CBD为等腰直角三角形,△CDM为含30°角的直角三角形,
根据BC=![]()
![]() ,可求得BD=CD=1,DM=
,可求得BD=CD=1,DM=![]()
![]() , .............................(9分)
, .............................(9分)
所以 BM =1+ ![]() ................................................(10分)
................................................(10分)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】把多项式3a2﹣9ab分解因式,正确的是( )
A. 3(a2﹣3ab) B. 3a(a﹣3b) C. a(3a﹣9b) D. a(9b﹣3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解中,是利用提公因式法分解的是( )
A. a2﹣b2=(a+b)(a﹣b) B. a2﹣2ab+b2=(a﹣b)2
C. ab+ac=a(b+c) D. a2+2ab+b2=(a+b)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x表示一个两位数,y表示一个三位数,把x放在y的左边,组成的五位数可表示为( )
A. x +y B. 100x+y C. 100x+1000 y D. 1000x+ y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com