
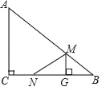
����Ŀ����ͼ��Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm������M�ӵ�B��������BA������ÿ��3cm���ٶ���A�˶���ͬʱ����N�ӵ�C��������CB������ÿ��2cm���ٶ����B�˶�����MG��BC���˶�ʱ��Ϊt�루0��t��![]() ��������MN��
��������MN��
��1���ú�t��ʽ�ӱ�ʾMG��
��2����tΪ��ֵʱ���ı���ACNM�������С���������С�����
��3������BMN���ABC���ƣ���t��ֵ��
���𰸡���1��MG��![]() t����2��t��2��ʱ��S�ı���ACNM��С��
t����2��t��2��ʱ��S�ı���ACNM��С��![]() cm2����3����BMN���ABC���ƣ�t��ֵΪ
cm2����3����BMN���ABC���ƣ�t��ֵΪ![]() ���
���![]() �룮
�룮
��������
��1�������ù��ɶ������AB��10�����жϳ���BGM�ס�BCA���ó�����ʽ���ɵó����ۣ�
��2���ȱ�ʾ��MN��������������ε������ɽ���������ϵʽ�����ɵó����ۣ�
��3���ȱ�ʾ��BM��BN���ٷ�����������������������εó�����ʽ����������⼴�ɵó����ۣ�
�⣺��1�����˶�֪��BM��3t��
��Rt��ABC��AC��6��BC��8��
��AB��10��
��MG��BC��
���MGB��90�㣽��ACB��
�ߡ�B����B��
���BGM�ס�BCA��
��![]() ��
��
��![]() ��
��
��MG��![]() t��
t��
��2�����˶�֪��CN��2t��
��BN��BC��CN��8��2t��
�ɣ�1��֪��MG��![]() t��
t��
��S�ı���ACNM��S��ABC��S��BNM��![]() BC��AC��
BC��AC��![]() BN��MG����8��6��
BN��MG����8��6��![]() ��8��2t����
��8��2t����![]() t��
t��![]() ��t��2��2+
��t��2��2+![]() ��
��
��0��t��![]() ��
��
��t��2��ʱ��S�ı���ACNM��С��![]() cm2��
cm2��
��3���ɣ�1����2��֪��BM��3t��BN��8��2t��
�ߡ�BMN����ABC���ƣ�
��ٵ���BMN��BACʱ��![]() ��
��
��![]() ��
��
��t��![]() �룬
�룬
�ڵ���BMN�ס�BCAʱ��![]() ��
��
��![]() ��
��
��t��![]() �룬
�룬
������BMN����ABC���ƣ�t��ֵΪ![]() ���
���![]() �룮
�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=5��OC=4��

��1����ͼ�٣���AB��ȡһ��D����ֽƬ��OD���ۣ�ʹ��A����BC���ϵĵ�E������D��E��������ꣻ
��2����ͼ�ڣ���OE����һ����P������O��E�غϣ����ӵ�O��������ÿ��1����λ���ٶ���OE�������E�����˶������˶�ʱ��Ϊt�루0��t��5��������P��PM��OE��OD�ڵ�M������ME����tΪ��ֵʱ���Ե�P��M��EΪ��������������ODA���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
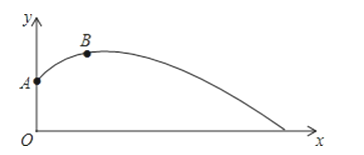
����Ŀ��С��Ϊ�˼���Լ�ʵ�����ѵ���������һ��Ͷ���IJ����У�ʵ��������������ͼ��ʾ�����г��ֵ�A������Ϊ��0��![]() ����������ߵ�B������Ϊ��3��
����������ߵ�B������Ϊ��3��![]() ����
����
��1���������ߵĽ���ʽ��
��2����֪ij������ʵ����ĵ÷ֱ������
�÷� | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
��Զ���ף� | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
����С���Ǵ�����ѧ���꼶����������С����ʵ����ѵ���еĵ÷֣�
��3����С����ϰʵ�������ǰ������Ͷ����7�״���һ������1.2��С��������ˣ���ʸ�С�����Ƿ���Σ�գ����ʵ������С��ͷ���Ϸ��ɳ�Ϊ��ȫ��������ΪΣ�գ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AO�ǡ�ABC�Ľ�ƽ���ߣ���OΪԲ�ģ�OCΪ�뾶����O��
��1����֤��AB�ǡ�O�����ߣ�
��2����֪AO����O�ڵ�E���ӳ�AO����O�ڵ�D��tanD=![]() ����
����![]() ��ֵ��
��ֵ��
��3����3�֣��ڣ�2���������£����O�İ뾶Ϊ3����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
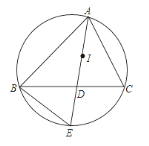
����Ŀ����ͼ��I�ǡ�ABC�����ģ�AI���ӳ��߽���BC�ڵ�D������ABC�����Բ�ڵ�E��
(1)BE��IE�������˵�����ɣ�
(2)����BI��CI��CE������BED=��CED=60���������ı���BECI�Ǻ��������ı��Σ���֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ģ���ǣ�������ɫ�����족��������ǿ���ƽ�����������ˮ��������������������ʩ������칤����Ϊ�ˣ�ij��������һ�ڹ�����ɺ�����4̨���ͺ�5̨������ˮ�����豸���������ʽ�102��Ԫ����ÿ̨�����豸�ļ۸��ÿ̨�����豸�۸���3��Ԫ����֪ÿ̨�����豸ÿ���ܴ�����ˮ240�֣�ÿ̨�����豸ÿ���ܴ�����ˮ180�֣�����ó����ڹ��̼�����ɣ���������ˮ��������ӣ����Ǹó������ٹ���ס��������豸��12̨���ڶ��ڹ��̵���ˮ������Ԥ�㱾�ι����ʽ���129��Ԫ��Ԥ�ƶ��ڹ�����ɺ�ÿ�½�����������2220����ˮ��
��1���������ÿ̨�����豸��ÿ̨�����豸�ļ۸���Ƕ�����Ԫ��
��2������������ڶ��ڹ��̵���ˮ�����豸�����й�����
��3������˵���ڣ�2�������з����У����ֹ������ܻ������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
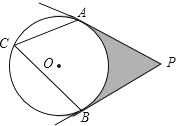
����Ŀ����ͼ��PA��PB�ֱ�����O������A��B���㣬��ACB=60�㣮
��1������P�Ķ�����
��2������O�İ뾶��Ϊ4cm����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
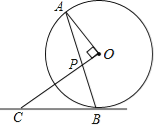
����Ŀ����ͼ��AB����O���ң�OP��OA��AB�ڵ�P������B��ֱ�߽�OP���ӳ����ڵ�C����CP=CB��
��1����֤��BC����O�����ߣ�
��2������O�İ뾶Ϊ![]() ��OP=1����BC�ij���
��OP=1����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
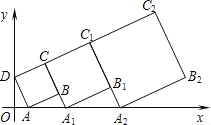
����Ŀ����ƽ��ֱ������ϵ�У���һ��������ABCD��λ����ͼ��ʾ����A������Ϊ��2��0������D������Ϊ��0��4�����ӳ�CB��x���ڵ�A1�����ڶ���������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������������A2B2C2C1�������������Ĺ��ɽ�����ȥ����2016�������ε����Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com