
 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 先判断出点A,B,D,C四点共圆即可得出①正确,用等腰直角三角形的性质和同弧所对的圆周角相等得出③正确,利用角平分线的性质定理和全等三角形的性质即可得出结论④正确,先求出∠BCD=∠CBD=22.5°,再判断出点C,E,D,G四点共圆,得出CG=CE,进而判断出CG=2CM,即可得出⑤正确,用三角形的面积公式和直角三角形的斜边大于直角边即可判断出②错误.
解答 解:如图,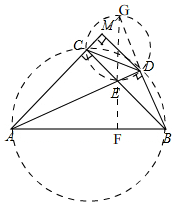 以AB为直径作圆,
以AB为直径作圆,
∵∠ACB=90°,BD⊥AE于D,
∴∠ACB=∠ADB=90°,
∴点A,B,D,C是以AB为直径的圆上,
∴∠CAD=∠CBD(同圆中,同弧所对的圆周角相等)
所以①正确;
在Rt△ABC中,AC=BC,
∴∠CAB=∠ABC=45°,
∴∠ADC=∠ABC=45°,
所以③正确;
过点E作EF⊥AB,
∵∠ACB=90°,AE平分∠BAC交BC于E,
∴CE=EF,
在Rt△BEF中,∠EBF=45°,
∴EF=FB,
∴CE=FB,
在Rt△AEC和Rt△AEF中,$\left\{\begin{array}{l}{CE=EF}\\{AE=AE}\end{array}\right.$,
∴Rt△AEC≌Rt△AEF,
∴AC=AF,
∴AB=AF+BF=AC+CE,
所以④正确;
∵AE平分∠BAC交BC于E,
∴∠CAE=∠BAD=$\frac{1}{2}$∠BAC=22.5°,
∴∠BCD=∠CBD=∠BAD=22.5°,
延长BD,AC相交于点G,
∵∠GCE=∠GDE=90°,
∴∠GCE+∠GDE=180°,
∴点C,E,D,G是以EG为直径的圆上,
连接EG,
在△ABG中,∠AGB=180°-∠BAC-∠ABC-∠CBD=67.5°,
∵∠DGE=∠DCE=22.5°,
∴∠AGE=∠AGD-∠DGE=45°,
在Rt△ECG中,∠AGE=45°,
∴CG=CE,
在△BAG中,AE平分∠BAG,AE⊥BG,
∴BD=GD,
∵BD=CD,
∴CD=GD,
∵DM⊥CG,
∴CG=2CM,
∴CE=2CM,
所以⑤正确;
∵CD是Rt△BCG的斜边的中线,
∴S△BCD=S△CDG=$\frac{1}{2}$CG×DM=$\frac{1}{2}$CE×DM
∵BC>CD>DM,
∴S△BCD=$\frac{1}{2}$CE×DM<$\frac{1}{2}$CE×BC,
∵S△ACE=$\frac{1}{2}$AC×CE=$\frac{1}{2}$BC×CE,
∴S△BCD<S△ACE,
所以②错误,
∴正确的又①③④⑤四个,
故选C.
点评 此题是三角形综合题,主要考查了四点共圆的判断,圆的性质,圆周角的性质,角平分线的性质,等腰三角形的性质和判定,全等三角形的性质和判定,解本题的关键是判断出四点共圆,是一道比较麻烦的压轴题,难点是判断CE=2CM.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | d>m | B. | d>$\frac{1}{2}$m | C. | d≥$\frac{1}{2}$m | D. | d≤$\frac{1}{2}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆上两点间的部分叫做弦 | |
| B. | 垂直于弦的直径平分弦,并且平分弦所对的两条弧 | |
| C. | 圆周角度数等于圆心角度数的一半 | |
| D. | 90度的角所对的弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{2}{x}$-1=0 | B. | 2x2-y-3=0 | C. | ax2-x+2=0 | D. | 3x2-2x-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com