
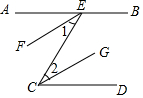
 填写证明的理由.
填写证明的理由.分析 根据平行线的性质得出∠AEC=∠DCE,根据角平分线定义得出∠1=$\frac{1}{2}$∠AEC,∠2=$\frac{1}{2}$∠ECD,求出∠1=∠2,根据平行线的判定得出即可.
解答 证明:∵AB∥CD(已知),
∴∠AEC=∠DCE( 两直线平行,内错角相等),
又∵EF平分∠AEC(已知),
∴∠1=$\frac{1}{2}$∠AEC( 角平分线定义),
同理∠2=$\frac{1}{2}$∠ECD,
∴∠1=∠2,
∴EF∥CG (内错角相等,两直线平行),
故答案为:两直线平行,内错角相等,AEC,角平分线定义,ECD,内错角相等,两直线平行.
点评 本题考查了角平分线定义和平行线的性质和判定的应用,能求出∠1=∠2是解此题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
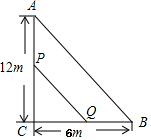 如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?
如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com