
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
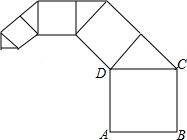 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
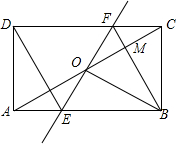 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
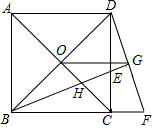 如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).
如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
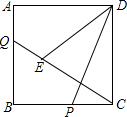 如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.
如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 出租车 | 滴滴打车 | 神州打车 |
| 3千米以内:12元 | 1.5元/千米 | 2元/千米 |
| 超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com