
【题目】为了迎接旅发大会顺利在织金召开,织金某巡警骑摩托车在南北大道上巡逻,一天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣4
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
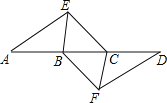
【题目】如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)求证:四边形 BFCE 是平行四边形.
(2)若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
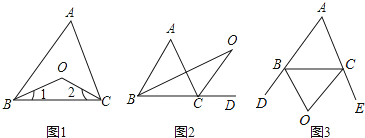
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ,理由如下:
,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB
∠ACB
∴∠1+∠2=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°-∠A
∴∠1+∠2=![]() (180°∠A)=90°
(180°∠A)=90°![]() ∠A
∠A
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,表示甲、乙两同学沿同一条路到达目的地过程中,路程S(千米)与时间t(小时)之间关系的图象,根据图象中提供的信息回答问题:
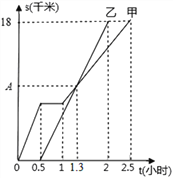
(1)乙的速度为_______千米/时;
(2)两人在乙出发后________小时相遇;
(3)点A处对应的数字为_________;
(4)甲在出发后1小时至2.5小时之间的速度为_________千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A、B分别表示的数是![]() 、
、![]() ,记A、B两点间的距离为AB
,记A、B两点间的距离为AB
(1) 若a=6,b=4,则AB= ;若a=-6,b=4,则AB= ;
(2) 若A、B两点间的距离记为![]() ,试问
,试问![]() 和
和![]() 、
、![]() 有何数量关系?
有何数量关系?
(3)写出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和.
(4)|x-1|+|x+2|取得的值最小为 ,|x-1|-|x+2|取得最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着改革开放进程的推进,改变的不仅仅是人们的购物模式,就连支付方式也在时代的浪潮中发生着天翻地覆的改变,除了现金、银行卡支付以外,还有微信、支付宝以及其他支付方式.在一次购物中,小明和小亮都想从微信、支付宝、银行卡三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com