练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知函数y=-（x-1）2图象上两点A（2，y1），B（a，y2），其中a＞2，则y1与y2的大小关系是y1＞y2（填“＜”、“＞”或“=”）

    分析 先根据函数的解析式得出函数的对称轴是直线x=1，开口向下，再进行比较即可．

    解答 解：∵函数y=-（x-1）2，
    ∴函数的对称轴是直线x=1，开口向下，
    ∵函数图象上两点A（2，y1），B（a，y2），a＞2，
    ∴y1＞y2，
    故答案为：＞．

    点评 本题考查了二次函数图象上点的坐标特征，能熟记二次函数的图象和性质内容是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．一个不透明的盒子中装有3个红球，2个白球，这些球除颜色外，没有任何其他区别，从这个盒子中同时随机摸出两个球，所有的可能性如下表：
    红球1红球2红球3白球1白球2
    红球1（红1，红2）（红1，红3）（红1，白1）（红1，白2）
    红球2（红2，红3）（红2，白1）（红2，白2）
    红球3（红3，白1）（红3，白2）
    白球1（白1，白2）
    白球2
    摸到两个红球的概率为（　　）
    A．$\frac{1}{10}$B．$\frac{1}{5}$C．$\frac{3}{10}$D．$\frac{2}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

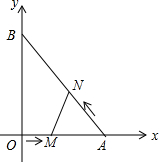    15．如图，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为（6，0），点B的坐标为（0，8）．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒$\frac{5}{3}$个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．
    （1）当t=3秒时，直接写出点N的坐标；
    （2）在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；
    （3）当t为何值时，△MNA是一个等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于点D，DE垂直平分AB，垂足为点E，请任意写出一组相等的线段BE=EA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列命题是假命题的是（　　）
    A．不在同一直线上的三点确定一个圆
    B．角平分线上的点到角两边的距离相等
    C．正六边形的内角和是720°
    D．角的边越大，角就越大

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列运算正确的是（　　）
    A．（x3）2=x5B．（-x）5=-x5C．x3•x2=x6D．3x2+2x3=5x5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率π的近似值，设半径为r的圆内接正n边形的周长为L，圆的直径为d，如图所示，当n=6时，π≈$\frac{L}{d}$=$\frac{6r}{2r}$=3，那么当n=12时，π≈$\frac{L}{d}$=3.11．（结果精确到0.01，参考数据：sin15°=cos75°≈0.259）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．计算$\frac{x}{x+1}$-$\frac{1}{x+1}$的结果为$\frac{x-1}{x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）计算：|2-$\sqrt{5}$|-$\sqrt{2}$（$\sqrt{\frac{1}{8}}$-$\frac{\sqrt{10}}{2}$）+$\frac{3}{2}$；
    （2）先化简，再求值：$\frac{x-2}{{x}^{2}+2x}$÷$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$+$\frac{1}{2x}$，其中x=-$\frac{6}{5}$．

    查看答案和解析>>

    同步练习册答案