【题目】现有七个数﹣1，﹣2，﹣2，﹣4，﹣4，﹣8，﹣8将它们填入图1（3个圆两两相交分成7个部分）中，使得每个圆内部的4个数之积相等，设这个积为m，如图2给出了一种填法，此时m＝64，在所有的填法中，m的最大值为_____．
科目：初中数学 来源： 题型：
【题目】某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有红星和巨星两家加工厂都想加工这批产品，已知红星厂单独加工比巨星厂单独加工这批产品多用20天，红星厂每天可加工16件产品，巨星厂每天可加工24件产品，公司需付给红星厂每天加工费800元，付给巨星厂每天加工费1200元．
这个公司要加工多少件新产品？
公司的产品可由一家工厂单独加工完成，也可由两家工厂合作完成，在加工过程中公司需另派一名工程师每天到厂家进行指导，并支付工程师每天10元的午餐补助，请你帮助公司从所有可供选择的方案中，选择一种既省钱又省时的加工方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图1，射线OP∥AE，∠AOP的角平分线交射线AE于点B．
（1）若∠A=50°，求∠ABO的度数；
（2）如图2，若点C在射线AE上，OB平分∠AOC交AE于点B，OD平分∠COP交AE于点D，∠ABO-∠AOB=70°，求∠ADO的度数；
（3）如图3，若∠A=α，依次作出∠AOP的角平分线OB，∠BOP的角平分线OB1，∠B1OP的角平分线OB2，…，∠Bn-1OP的角平分线OBn，其中点B，B1，B2，…，Bn-1，Bn都在射线AE上，试求∠ABnO的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，四边形ABED的面积为6，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，从点A看一山坡上的电线杆PQ，观测点P的仰角是45°，向前走6m到达B点，测得顶端点P和杆底端点Q的仰角分别是60°和30°，求该电线杆PQ的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
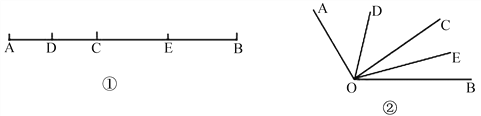
【题目】如图①，已知线段AB=12cm，点C为线段AB上的一个动点，点D、E分别是AC和BC的中点．
（1）若点C恰好是AB的中点，则DE= cm；若AC=4cm，则DE= cm；
（2）随着C点位置的改变，DE的长是否会改变？如果改变，请说明原因；如果不变，请求出DE的长；
（3）知识迁移：如图②，已知∠AOB=120°，过角的内部任意一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE的度数与射线OC的位置无关．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面三行数：
第1列 | 第2列 | 第3列 | 第4列 | … | 第n列 |
﹣3 | 9 | a | 81 | … | r |
1 | ﹣3 | 9 | b | … | s |
﹣2 | 10 | c | 82 | … | t |
（1）直接写出a，b，c的值；
（2）直接写出r，s，t的值；
（3）设x，y，z分别为第①②③行的第2019个数，求x+6y+z的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形OABC是平行四边形，点C在x轴上，反比例函数y= 
（x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为 ．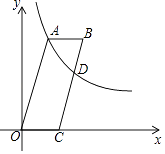 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
小明遇到这样问题：
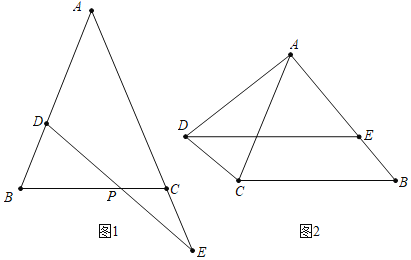
如图1，在
中，
，在AB上取一点D，在AC延长线上取一点E，若
，判断PD与PE的数量关系．
小明通过思考发现，可以采用两种方法解决向题：
方法一：过点D作
，交BC于F，即可解决向题；
方法二：过点D、点E分别向直线BC引垂钱，垂足分别是F、G，也可解决问题．
请回答：PD与PE的数量关系是______；
任选上述两种方法中的一种方法，在图1中补全图象，并给出证明；
参考小明思考问题的方法，解决问题：
如图2，在中，
，将AC绕点A顺时针旋转
度后得到AD，过点D作
，交AB于点E，
，则图中是否存在与DE相等的线段，请找出来并给出证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
