
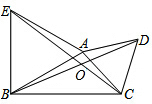
 如图,在△ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD与CE相交于点O.
如图,在△ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD与CE相交于点O.分析 (1)根据等边三角形的性质得:AE=AB,AC=AD,∠EAB=∠CAD=60°,所以∠EAC=∠BAD,可以证明△AEC≌△ABD,则EC=BD;
(2)添加条件:AB=AC,则两个等边三角形的6条边相等,则△ABE和△ACD全等,并根据外角的性质可知:∠BOC=∠OCD+∠BDC=120°.
解答 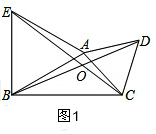 解:(1)如图1,EC=BD,理由是:
解:(1)如图1,EC=BD,理由是:
∵△ABE、△ACD都是等边三角形,
∴AE=AB,AC=AD,∠EAB=∠CAD=60°,
∴∠EAB+∠BAC=∠CAD+∠BAC,
即∠EAC=∠BAD,
∴△AEC≌△ABD,
∴EC=BD;
(2)添加条件:AB=AC,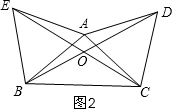 如图2,
如图2,
∵AE=AB=BE,AC=AD=CD,
∴AE=AB=BE=AC=AD=CD,
∴△ABE≌△ACD;
由(1)得:△AEC≌△ABD,
∴∠BDA=∠ECA,
∴∠ECA+∠BDC=∠BDA+∠BDC,
∵∠BOC=∠OCD+∠BDC,
∴∠BOC=∠ECA+∠ACD+∠BDC=∠BDA+∠BDC+∠ACD=120°;
∴整个图形是轴对称图形,此时∠BOC=120°.
点评 本题考查了等边三角形、轴对称、全等三角形的性质和判定,是常考题型,两个等边三角形能构建一对全等三角形,只需说明其夹角相等即可得出全等.


科目:初中数学 来源: 题型:选择题
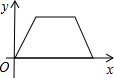 如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )| A. | 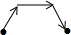 | B. |  | C. | 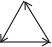 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com