
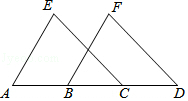
 已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.
已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.分析 (1)易证AC=BD,根据SSS推出△AEC≌△BFD,根据全等三角形的性质得出∠A=∠FBD即可;
(2)因为∠ACE=∠BDF,根据平行线的判定推出即可.
解答 解:(1)∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
在△AEC和△BFD中
$\left\{\begin{array}{l}{AE=BF}\\{AC=BD}\\{CE=DF}\end{array}\right.$
∵△AEC≌△BFD(SSS),
∴∠A=∠FBD,
∴∠A=∠FBD,
∵∠A=60°,
∴∠FBD=60°;
(2)证明:
∵△AEC≌△BFD,
∴∠ACE=∠BDF,
∴EC∥DF.
点评 本题考查了全等三角形的性质和判定,平行线的判定的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )| A. | 5:8 | B. | 3:8 | C. | 3:5 | D. | 2:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)
如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
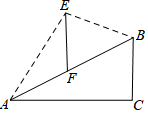 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )| A. | 16.9 米 | B. | 13.7米 | C. | 14.6米 | D. | 15.2米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
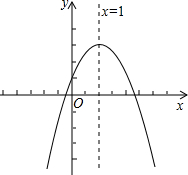 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
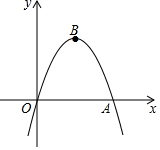 如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com