
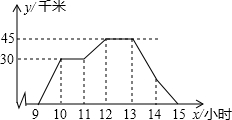
 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由函数图象可知:骑车人9:00出发,12时到达B地,15时返回A地,则应用平均速度=$\frac{总路程}{总时间}$可求得问题①、③;客车11:15追上骑车人意味着在同一时刻他们与A地
距离相等,由此可以分析求解②;问题④涉及相遇问题,搞清楚他们何时相遇即可.
解答 解:①∵点(12,45)表示骑车人在12时距离A地45千米,而A、B两地路程为45,
∴①骑车人12点到达B地说法正确;
②∵11:15客车已经行驶了45分钟=$\frac{3}{4}$小时,则客车行驶的路程是:45×$\frac{3}{4}$=33.75(千米),
而此时骑车人行驶时间为:11:15-9:00=2$\frac{1}{4}$小时,其行驶路程为:30+15×$\frac{1}{4}$=33.75(千米),
∴客车11:15追上骑车人,即:②说法正确;
③∵骑车人整个运动过程所用时间15-9=6(小时),行程为45×2=90(千米),
∴骑车人的平均速度为:90÷6=15千米/时
故:③的说法正确;
④∵由题意可知,客车到达B地用1小时,而此时骑车人还未到达,
又客车在11:30到达B地,而此时骑车人距离B地45-30-15×$\frac{1}{2}$=7.5(千米),
设客车返回后t小时与骑车人相遇,则:
45t+15t=7.5
解之得,t=$\frac{1}{8}$
故:选C
点评 本题考查了函数图象及其应用;解题的关键是要审清楚图象所反应的整个运动过程及其所对应的x与y的值.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
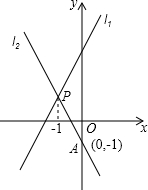 如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=3 | B. | x=0 | C. | x=2 | D. | x=a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$.
如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为$\frac{7}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com