
����Ŀ��ij��ݹ�˾�мס�������������ͬһ·�ߴ�A�ص�B�����ͻ��ij������ͬʱ��A�س�����ʻ��B�أ�;���ҳ����ڳ��ֹ��ϣ�ͣ��������һ��ʱ�䣬������Ϻ��ҳ��ӿ����ٶ�����ʻ��B�أ��׳���A�ص�B���ٶ�ʼ�ձ��ֲ��䣮��ͼ��ʾ�Ǽס�������֮��ľ���y(km)����������ʱ��x(h)�ĺ���ͼ���������Ϣ����������⣺
(1)��M�������ʾ��ʵ��������ʲô��
(2)���MN����ʾ�Ĺ�ϵʽ����д���ҹ��Ϻ���ٶȣ�
(3)�����ǰ�������ٶ��Լ�a��ֵ��
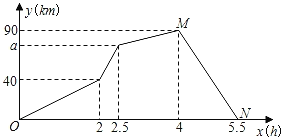
���𰸡�(1) ����ʻ4Сʱʱ���׳�����B��(�յ�)���ҳ������յ㻹��90ǧ�ף�(2) y=��60x+330��60ǧ��/Сʱ��(3) �׳��ٶ�Ϊ70ǧ��/Сʱ����Ϊ50ǧ��/Сʱ��a��ֵΪ75
��������
(1)�۲�ͼ������������ɵô𰸣�
(2)��MN����ʾ�Ĺ�ϵʽΪy=kx+b���ô���ϵ�������ý���ʽ������·�̳�����Ӧ��ʱ��ɵ��ٶȣ�
(3)�����ʱ���ٶ�Ϊvǧ��/Сʱ�����ٶ�Ϊ(v��20)ǧ��/Сʱ�������ҳ����ֹ��Ϻ��(2.5��2)Сʱ�׳���ʻ��·�̼����ҳ������ų�����������������ľ������90ǧ��ȥ40ǧ�ף��г�����v�ķ��̣����v��ֵ�����ҳ��ٶ�Ҳ����ã�Ȼ����40+70��0.5���㼴�ɵó�a��ֵ��
�⣺(1)�𣺵�M�������ʾ��ʵ�������ǣ�����ʻ4Сʱʱ���׳�����B��(�յ�)���ҳ������յ㻹��90ǧ�ף�
(2)��MN����ʾ�Ĺ�ϵʽΪy=kx+b����M(4��90)��N(5.5��0)����ã�
![]() ��
��
��ã�![]() ��
��
��MN����ʾ�Ĺ�ϵʽΪy=��60x+330��
�����ų����ҳ��ٶ�Ϊ��90��(5.5��4)=60ǧ��/Сʱ��
(3)��40��2=20ǧ��/Сʱ��
�������ʱ���ٶ�Ϊvǧ��/Сʱ�����ٶ�Ϊ(v��20)ǧ��/Сʱ�����У�
(2.5��2)v+(4��2.5)(v��60)=90��40��
��ã�v=70��
���׳��ٶ�Ϊ70ǧ��/Сʱ����Ϊ50ǧ��/Сʱ��
��a��ֵΪ40+70��0.5=75��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ��ĶԳ���Ϊֱ��
��ͼ��ĶԳ���Ϊֱ��![]() ���������£�����
���������£�����![]() ������е�һ��������
������е�һ��������![]() �����н��ۣ���
�����н��ۣ���![]() ;��
;��![]() ;��
;��![]() ;��
;��![]() ��ȷ�ĸ����ǣ� ��
��ȷ�ĸ����ǣ� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ��ȤС���У������������λͬѧ�������ͼ��ʾ������ת������Ϸ��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿ�����������ڱ������֣�����Ϸ�������£����˷ֱ�ͬʱת���ס���ת�̣�ת��ֹͣ����ָ����ָ������������С��12���������ʤ����ָ����ָ�����������͵���12����Ϊƽ�֣���ָ����ָ�����������ʹ���12����������ʤ����ָ��ͣ�ڵȷ����ϣ���תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ����
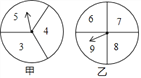
��1�������б��ķ�����ʾ��������Ϸ�������͵����п��ܵĽ����
��2���ֱ���������������ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
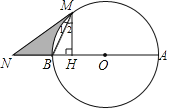
����Ŀ����ͼ��AB�ǡ�O��ֱ����NM���O�����ڵ�M����AB���ӳ��߽��ڵ�N��MH��AB�ڵ�H��
��1����֤����1����2��
��2������N��30����BN��5�����O�İ뾶��
��3���ڣ�2���������£����߶�BN��MN���ӻ�BMΧ�ɵ���Ӱ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
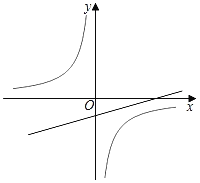
����Ŀ����ͼ����ƽ��ֱ������ϵ��AΪֱ��y=![]() x��1��һ�㣬��ԭ��O��ֱ���뷴��������y=��
x��1��һ�㣬��ԭ��O��ֱ���뷴��������y=��![]() ͼ���ڵ�B��C������ABCΪ�ȱ������Σ����A������Ϊ_____��
ͼ���ڵ�B��C������ABCΪ�ȱ������Σ����A������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ�����ɫ��ͬ�ĺ���ͺ�������һ�������Ĵ�����װ��2�������2������
��1���������һ�����Ǻ���ĸ���Ϊ �����ȴӴ�����ȡ��m�������Żأ����ٴӴ������������һ������������������Ϊ�¼�A�����¼�AΪ��Ȼ�¼�����m�� ��
��2�����Ӵ�����һ���������������б�������״ͼ���г����еȿ��ܽ��������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������3��4��4��5��������һ����4�������仯��ͳ������( )
A.ƽ����B.����C.��λ��D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻУ�Ļ�������ѧ�����ۺ����ʣ��ٽ���ѧ��ȫ�淢չ��ѧУ��չ�˶������Ż��С��ϲ���������У��ϳ����š��������š��鷨���š��Ƽ����ţ��ֱ�����ĸA��B��C��D���α�ʾ���ĸ����ţ����������ĸ���ĸ�ֱ�д��������ȫ��ͬ�IJ����Ŀ�Ƭ�������ϣ�Ȼ�������ſ�Ƭ���泯��ϴ�Ⱥ���������ϣ�
��1��С�����������ȡһ�ſ�Ƭ����������B�ĸ������� ����
��2��С���ȴ��������ȡһ�ſ�Ƭ����¼�¿�Ƭ�ϵ���ĸ�Żأ��ٴ�ʣ��Ŀ�Ƭ�������ȡһ�ſ�Ƭ����¼�¿�Ƭ�ϵ���ĸ���������б�������״ͼ�����С�����γ�ȡ�Ŀ�Ƭ����һ���ǿƼ�����D�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
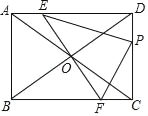
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4�����Խ���AC�ƶԽ��߽���O��ת���ֱ�AD��BC�ڵ�E��F����P�DZ�DC�ϵ�һ�����㣬�ұ���DP��AE������PE��PF����AE��x��0��x��3����
��1����գ�PC���� ����FC���� �������ú�x�Ĵ���ʽ��ʾ��
��2�����PEF�������Сֵ��
��3�����˶������У�PE��PF�Ƿ�����������������x��ֵ��������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com