
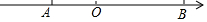 如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.
如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.分析 (1)由题意k=-1,A、B两点所表示的有理数分别为-6,8,所以AB=6+8=14;
(2)由P点表示的数为-6+3t,Q点表示是数为8-4t,PM=QM,可得M点表示的数为$\frac{-6+3t+8-4t}{2}$=$\frac{2-t}{2}$;
(3)由题意PQ=6,可得|(8-4t)-(-6+3t)|=6,解方程求出t即可解决问题;
解答 解:(1)由题意k=-1,A、B两点所表示的有理数分别为-6,8,所以AB=6+8=14.
(2)∵P点表示的数为-6+3t,Q点表示是数为8-4t,PM=QM,
∴M点表示的数为$\frac{-6+3t+8-4t}{2}$=$\frac{2-t}{2}$.
(3)由题意PQ=6,
∴|(8-4t)-(-6+3t)|=6,
解得t=$\frac{8}{7}$或$\frac{20}{7}$.
此时PB=$\frac{74}{7}$或$\frac{38}{7}$.
点评 本题考查一元一次方程的应用、数轴、路程、速度、时间之间的关系等知识,解题的关键是理解题意,学会构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果整数a是整数b的倍数,那么b是a的因数 | |
| B. | 一个合数至少有3个因数 | |
| C. | 在正整数中,除2外所有的偶数都是合数 | |
| D. | 在正整数中,除了素数都是合数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).
如图,在平面内直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC,点E是y轴上任意一点,记点E为(0,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
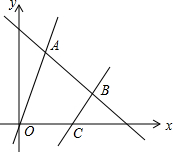 如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.
如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象是一条直线 | B. | y有最大值 | ||
| C. | y有最小值 | D. | y既没有最大值也没有最小值 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{2}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=-$\frac{6}{x}$ | D. | y=-$\frac{3}{2x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com