
【题目】如图,折线![]() 中,
中,![]() ,
,![]() ,将折线
,将折线![]() 绕点
绕点![]() 按逆时针方向旋转,得到折线
按逆时针方向旋转,得到折线![]() ,点
,点![]() 的对应点落在线段
的对应点落在线段![]() 上的点
上的点![]() 处,点
处,点![]() 的对应点落在点
的对应点落在点![]() 处,连接
处,连接![]() ,若
,若![]() ,则
,则![]() _____°.
_____°.
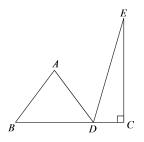
【答案】![]()
【解析】
连接AC 、AE ,过点A作AF⊥BC于F ,作AH⊥EC于H.再证明四边形AFCH是矩形,可得AF=CH ,由旋转的性质可得AD=AB=3、BC=DE=5,∠ABC=∠ADE,则△ABC≌△ADE,即AC=AE ;再由等腰三角形的性质和勾股定理可得BF、AF、EC、CD的长,最后根据正切定义解答即可.
解:如图:连接AC 、AE ,过点A作AF⊥BC于F ,作AH⊥EC于H.
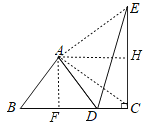
∵CE⊥BC,AF⊥BC,AH⊥EC
∴四边形AFCH是矩形,
∴AF=CH,
∵将折线AB-BC绕点A按逆时针方向旋转,得到折线AD-DE
∴AD=AB=3、BC=DE=5,∠ABC=∠ADE
∴△ABC≌△ADE
∴AC=AE,
∵AC=AE,AB=AD,AF⊥BC,AH⊥EC,BF=DF,CH=EH
∴![]()
∴![]()
∴BF=![]() ,AF=
,AF=![]()
∴![]()
∴![]()
故答案为:2


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
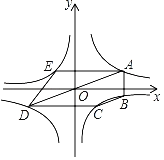
【题目】如图,经过原点O的直线与反比例函数y=![]() (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=
(a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=![]() (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,
(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,![]() 的值为__.
的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了优化环境,将对某一小区环境进行绿化,现有甲、乙两家绿化公司进行了投标,各自推出了绿化收费方案如下:甲公司绿化费用![]() (元) 与绿化面积
(元) 与绿化面积![]() (平方米)是一次函数关系,如图所示。
(平方米)是一次函数关系,如图所示。
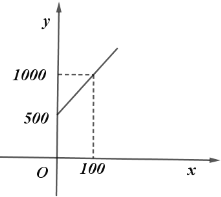
乙公司:绿化面积不超过1000平方米时,统一收取费用5000元;绿化面积超过1000平方米时,超过部分每平方米收取3元.
(1)求甲、乙公司绿化费用![]() (元)与绿化面积
(元)与绿化面积![]() (平方米)的函数表达式;
(平方米)的函数表达式;
(2)如果该小区目前的绿化面积是1500平方米,试通过计算说明:选择哪家公司的绿化费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:再探平行四边形的性质
问题情境:
学完平行四边形的有关知识后,同学们开展了再探平行四边形性质的数学活动,以下是“希望小组”得到的一个性质:
如图1,已知平行四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 于点
于点![]() ,则
,则![]() .
.
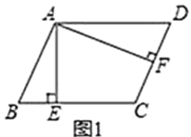
问题解决:
(1)如图2,当![]() 时,
时,![]() 还成立吗?证明你发现的结论;
还成立吗?证明你发现的结论;
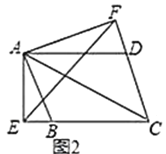
(2)如图2,连接![]() 和
和![]() ,若
,若![]() .求
.求![]() 的度数;
的度数;
(3)如图3,若![]()
![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() .则
.则![]() _________
_________![]() .(用含
.(用含![]() 的三角函数表示)
的三角函数表示)
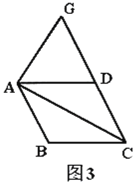
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 的边上按
的边上按![]() 的路线匀速移动,当点
的路线匀速移动,当点![]() 到达
到达![]() 点时停止移动;动点
点时停止移动;动点![]() 以
以![]() 的速度在
的速度在![]() 的边上按
的边上按![]() 的路线匀速移动,当点
的路线匀速移动,当点![]() 到达
到达![]() 点时停止移动.已知点
点时停止移动.已知点![]() 、点
、点![]() 同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点
同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点![]() 移动的时间为
移动的时间为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
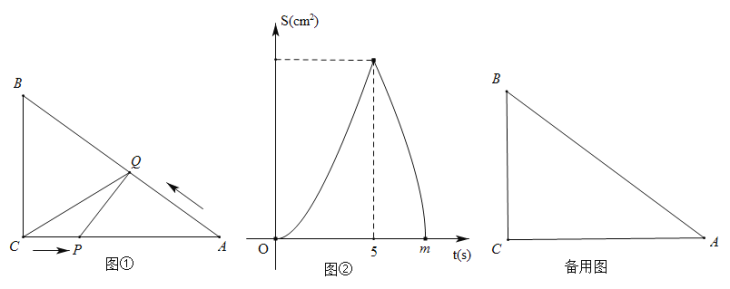
(1)图①中![]()
![]() ,图②中
,图②中![]()
![]() ;
;
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论个数是( )
;其中正确的结论个数是( )
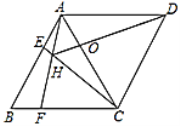
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com