练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某完全中学（含初、高中）篮球队12名队员的年龄情况如下：

    年龄（单位：岁）

    14

    15

    16

    17

    18

    人　数

    1

    4

    3

    2

    2

    （1）这个队队员年龄的众数是　　　　　　，中位数是　　　　　　；

    （2）求这个队队员的平均年龄；

    （3）若把这个队队员年龄绘成扇形统计图，请求出年龄为15岁对应的圆心角的度数．

    【答案】（1）15，16；（2）16；（3）120°

    【解析】试题分析：（1）众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据定义即可求解；

    （2）利用求平均数公式计算即可；

    （3）年龄为15岁所占的百分比，乘以360即可得到结果．

    试题解析：1）15岁出现了4次，次数最多，因而众数是：15；

    12个数，处于中间位置的都是16，因而中位数是：16．

    （2）这个队队员的平均年龄==16（岁）；

    （3）年龄为15岁对应的圆心角的度=×360°=120°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商店一套服装进价为300元，如果按标价的八折销售可获利80元，那么该服装的标价是（ ）
    A.375元
    B.380元
    C.450元
    D.475元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABC中，AP=DP，DE=DF，DE⊥AB于E，DF⊥AC于F，则下列结论：①.AD平分∠BAC；②.△BED≌△FPD；③.DP∥AB；④.DF是PC的垂直平分线．其中正确的是= _________ .（写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y＝ax5+bx3+cx+14．当x＝n时，y＝20，则当x＝﹣n时，y的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 正六边形的每一个内角的度数是___________°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个车间加工轴杆和轴承，平均每人每天可以加工轴杆12根或轴承15个．车间共90人，应该怎样分配人，才能使每天生产的轴杆和轴承正好配套（一根轴杆和一个轴承恰好配成一套）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB =AC=2，∠B = 40°，点D在线段BC上运动（不与点B，C重合），连接AD，作∠ADE = 40°，DE交线段AC于点E．

    （1）当∠BDA = 115°时，∠BAD= °，∠DEC = °，当点D从点B向点C运动时，∠BDA逐渐变 （填“大”或“小”） ．

    （2）当DC等于多少时，△ABD≌△DCE？请说明理由．

    （3）在点D的运动过程中，是否存在△ADE是等腰三角形？若存在，请直接写出此时∠BDA的度数；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

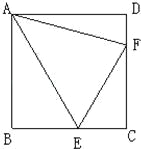
    【题目】如图，正方形ABCD中，AB＝，点E、F分别在BC、CD上，且∠BAE＝30°，∠DAF＝15度．

    （1）求证：DF＋BE＝EF；

    （2）求∠EFC的度数；

    （3）求△AEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（11分）如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F. 点D、E的坐标分别为（0，6），（-4，0），连接PD，PE，DE.

    （1）请直接写出抛物线的解析式；

    （2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值. 进而猜想：对于任意一点P，PD与PF的差为定值. 请你判断该猜想是否正确，并说明理由；

    （3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE的周长最小时“好点”的坐标.

    查看答案和解析>>

    同步练习册答案