
【题目】如图,等腰 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 于点
于点 ![]() ,点
,点 ![]() 是
是 ![]() 延长线上一点,点
延长线上一点,点 ![]() 是线段
是线段 ![]() 上一点,
上一点, ![]() ,
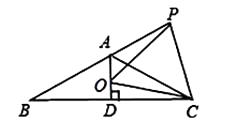
,
下面结论:
① ![]() ;
;
② ![]() 是等边三角形;
是等边三角形;
③ ![]() ;
;
④ ![]() .
.
其中正确的是( ).
A.②③
B.①②④
C.③④
D.①②③④
【答案】D
【解析】连接OB,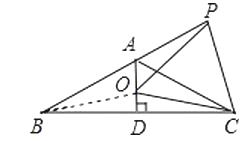
∵AB=AC,AD⊥BC,∴OB=OC, BD=CD,∠BAD= ![]() ∠BAC=
∠BAC= ![]() ×120°=60°,∴∠ABC=90°-∠BAD=30°,
×120°=60°,∴∠ABC=90°-∠BAD=30°,
∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;故①正确;
∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形;故②正确;在AC上截取AE=PA,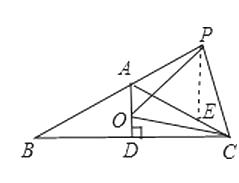
∵∠PAE=180°-∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,
在△OPA和△CPE中, 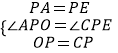 ,∴△OPA≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
,∴△OPA≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;
过点C作CH⊥AB于H,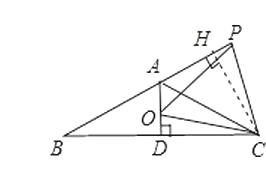
∵∠PAC=∠DAC=60°,AD⊥BC,∴CH=CD,
∴S△ABC= ![]() AB·CH,S四边形AOCP=S△ACP+S△AOC=
AB·CH,S四边形AOCP=S△ACP+S△AOC= ![]() AP·CH+
AP·CH+ ![]() OA·CD
OA·CD
= ![]() AP·CH+
AP·CH+ ![]() OA·CH=
OA·CH= ![]() CH·(AP+OA)=
CH·(AP+OA)= ![]() CH=·AC,
CH=·AC,
∴S△ABC=S四边形AOCP;
故④正确.所以①②③④都正确,故答案为:D.
连接OB,可证明①②正确,在AC上截取AE=PA,可证③正确,过点C作CH⊥AB于H,可证④正确。


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
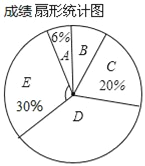
【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |
(1)频数分布表中的m= ,n= ;
(2)样本中位数所在成绩的级别是 ,扇形统计图中,E组所对应的扇形圆心角的度数是 ;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科学技术协会为倡导青少年主动进行研究性学习,积极研究身边的科学问题,组织了以“体验、创新、成长”为主题的青少年科技创大赛,在层层选拔的基础上,所有推荐参赛学生分别获得了一、二、三等奖和纪念奖,工作人员根据获奖情况绘制成如图所示的两幅不完整的统计图,根据图中所给出的信息解答下列问题:
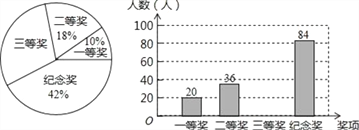
(1)这次大赛获得三等奖的学生有多少人?
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示三等奖扇形的圆心角是多少度?
(4)若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
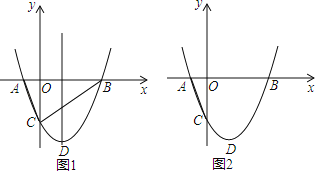
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;
(4)在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )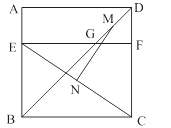
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com