
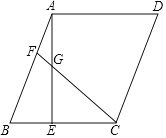
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
【答案】(1)![]() 1;(2)见解析.
1;(2)见解析.
【解析】
(1)在Rt△ABE中,由勾股定理求得BE,再由线段和差求得结果;
(2)延长GA到H,使得AH=BE,证明△ADH≌△EAB得DH=AB=CD,得∠DCH=∠DHC,再证明∠GHC=∠GCH得GC=GH便可得结果.
(1)∵CF=CB=AE,BC![]() ,
,
∴AE![]() ,
,
∵AE⊥BC于点E,AB![]() ,
,
∴BE![]() ,
,
∴CE=BC﹣BE![]() 1;
1;
(2)延长GA到H,使得AH=BE,连接DH,CH,
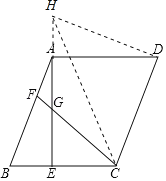
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE⊥BC,
∴∠AEB=∠DAE=90°,
∵BC=AE,
∴AE=DA,
在△ADH和△EAB中,
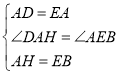 ,
,
∴△ADH≌△EAB(SAS),
∴DH=DC,∠DHA=∠ABE,
∴∠DHC=∠DCH,
∵CB=CF,
∴∠CBF=∠CFB,
∵AB∥CD,
∴∠CFB=∠DCF,
∴∠CBF=∠DCF,
∵∠DHA=∠ABE,
∴∠DHA=∠DCF,
∵∠DHC=∠DCH,
∴∠CHG=∠HCG,
∴CG=HG,即CG=AG+AH,
∴AH=CG﹣AG,
∵AH=BE,
∴BE=CG﹣AG,


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果的单价是多少元?
(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市决定购进甲、乙两种取暖器,已知甲种取暖器每台进价比乙种取暖器多500元, 用40000元购进甲种取暖器的数量与用30000元购进乙种取暖器的数量相同.请解答下列问题:
(1)求甲、乙两种取暖器每台的进价;
(2)若甲种取暖器每台售价2500元,乙种取暖器每台售价1800元,超市欲同时购进两种取暖器20 台,且全部售出.设购进甲种取暖器x(台),所获利润为y(元),试用关于x的式子表示y;
(3)在(2)的条件下,若超市计划用不超过36000元购进取暖器,且甲种取暖器至少购进10台, 并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器. 求购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ABCD 的对角线 AC 、 BD 相交于点O , BD 12cm , AC 6cm ,点 E 在线段 BO 上从点 B 以1cm / s 的速度向点 O 运动,点 F 在线段OD 上从点O 以 2cm / s 的速度向点 D 运动.
(1)若点 E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形 AECF 是平行四边形.
(2)在(1)的条件下,当 AB 为何值时, AECF 是菱形;
(3)求(2)中菱形 AECF 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据: ![]() ,
, ![]() )
)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级选派甲、乙两位同学参加学校的跳远比赛,体育老师对他们的5次训练成绩进行了整理,并绘制了不完整的统计图,如图所示,请根据图中信息,解答下列问题:
甲、乙两人跳远成绩统计表:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩/厘米 | 588 | 597 | 608 | 610 | 597 |
乙成绩/厘米 | 613 | 618 | 580 | a | 618 |
根据以上信息,请解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)通过计算,补充完整下面的统计分析表;
运动员 | 最好成绩 | 平均数 | 众数 | 方差 |
甲 |
|
| 597 | 41.2 |
乙 | 618 | 600.6 |
| 378.24 |
(4)请依据(3)中所统计的数据分析,甲、乙两位同学的训练成绩各有什么特点.

查看答案和解析>>
科目:初中数学 来源: 题型:
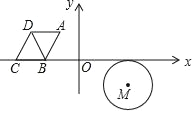
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上两点![]() 分别表示有理数2和5,我们用
分别表示有理数2和5,我们用![]() 来表示
来表示![]() 两点之间的距离.
两点之间的距离.
![]()
(1)直接写出![]() 的值=______;
的值=______;
(2)若数轴上一点![]() 表示有理数m,则
表示有理数m,则![]() 的值是______;
的值是______;
(3)当代数式∣n +2∣+∣n 5∣的值取最小值时,写出表示n的点所在的位置;
(4)若点![]() 分别以每秒2个单位长度和每秒3个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点
分别以每秒2个单位长度和每秒3个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点![]() 到原点的距离是点
到原点的距离是点![]() 到原点的距离的2倍.
到原点的距离的2倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com