
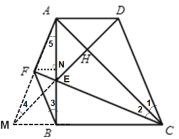
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE的延长线于F.连接DE交对角线AC于H.下列结论:①AC垂直平分ED;②AE=BE;③CE=2BF;④BE=2EF.其中结论正确的是_______.(填序号)

【答案】①③
【解析】
根据△ABC是等腰直角三角形,得出∠BAC=∠BCA=45°,再由AD∥BC得出AC平分∠EAD,又因为AE=AD所以AC是DE的垂直平分线即AC垂直平分ED;延长AF和CB交于点M,连接EM,F、A、B、C四点共圆,F、E、B、M四点共圆,AE=ME>BE;由△AMB≌△CEB, 得出BF=![]() AM,即CE=2BF;作FN∥MB,推出BE<2EF.
AM,即CE=2BF;作FN∥MB,推出BE<2EF.
解:∵∠ABC=90°,AB=BC
∴△ABC是等腰直角三角形
∴∠BAC=∠BCA=45°
∵AD∥BC,
∴∠CAD=∠BCA
∴∠BAC=∠CAD
∴AC平分∠EAD
∵AE=AD
∴AC垂直平分ED①正确;
延长AF和CB交于点M,连接EM,M、E、D在一条直线上,
由F、A、B、C四点共圆,F、E、B、M四点共圆,
可得∠1=∠2=∠3=∠4,∠FBM=45°+∠1, ∠FMB=45°+∠4,
∴FM=FM,FA=FB, ∠5=∠3=∠4,AE=ME>BE故②不成立;由△AMB≌△CEB,可得CE=AM,F是MA的中点,BF=![]() AM, ∴CE=2BF,故③成立;作FN∥MB,可得BE=BM=2FN,故FN<EF,故BE<2EF,④不成立;故答案为:①③.
AM, ∴CE=2BF,故③成立;作FN∥MB,可得BE=BM=2FN,故FN<EF,故BE<2EF,④不成立;故答案为:①③.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】在不透光的布袋里放入标有数字2,0,﹣3的三张的卡片(形状与质地完全相同).现在随机地抽出两张卡片,将两个数字分别记作某个点的横坐标与纵坐标.
(1)从布袋中同时抽取两张卡片时组成的所有点中,直接写出“点落入第四象限”概率是 ;
(2)如果抽出第一张卡片记录数字后放回布袋,再从袋中抽取第二张卡片记录数字后组成一个点,用画树状图或列表法,求出“点落在坐标轴上”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图钢架中,∠AOB=10°,要使钢架更加牢固,需在其内部添加一些钢管:EF,FG,GH…,且OE=EF=FG=GH…,在OA,OB 足够长的情况下,最多能添加这样的钢管的根数为 ( ).

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=![]() ,则AE2+BE2的值为 ( )
,则AE2+BE2的值为 ( )

A. 8 B. 12 C. 16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
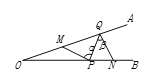
【题目】如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P,Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β-α的值为( )
A.19°B.40°C.9°D.29
查看答案和解析>>
科目:初中数学 来源: 题型:
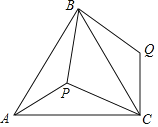
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com