
由二次函数y=﹣x2+2x可知( )
A. 图象是开口向上的 B. 对称轴为x=﹣1 C. 最大值为1 D. 顶点坐标为(﹣1,1)
C 【解析】试题解析:∵y=﹣x2+2x=﹣(x﹣1)2+1, ∴抛物线的开口向下,A错误; 对称轴为直线x=1,B错误; 当x=1时,函数取得最大值1,C正确; 顶点坐标为(1,1),D错误; 故选:C 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:填空题
若一个圆锥的侧面展开图是一个半径为3cm,圆心角为120°的扇形,则该圆锥的侧面面积为_____cm2(结果保留π).
3π 【解析】.查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
解方程:
(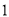 )
) .
.
( )
) .
.
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列各式中,去括号正确的是( ).
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:填空题
抛物线y=2x2﹣bx+3的对称轴是直线x=1,则b的值为 .
4. 【解析】试题考查知识点:抛物线y=ax2+bx+c(a≠0)的对称轴是直线 思路分析:直接套用对称轴解析式即可得到关于系数b的方程 具体解答过程: ∵抛物线y=ax2+bx+c(a≠0)的对称轴是直线,抛物线y=2x2-bx+3的对称轴是直线x=1 ∴ 解之得:b=4查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
一般情况下,一个分式通过适当的变形,可以化为整式与分式的和的形式,例如:
① ;
;
②
(1)试将分式 化为一个整式与一个分式的和的形式;
化为一个整式与一个分式的和的形式;
(2)如果分式 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
(1)计算:(a-1)²-a(a-1); (2)分解因式:xy²-4x;
(1)-a+1;(2)x(y+2)(y-2). 【解析】试题分析:(1)先去括号,再进行加减运算即可;(2)先提取公因式x,然后用平方差公式因式分解. 试题解析: (1)原式=a2-2a+1-a2+a=-a+1; (2)原式=x(y²-4)=x(y+2)(y-2).查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
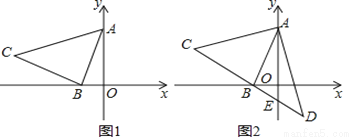
如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC .
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(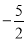 ,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的
,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的 ?若存在,请求出点N的坐标;若不存在,请说明理由.
?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
已知 ,则代数式
,则代数式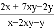 的值为__________.
的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com